理学部ニュース
理学部ニュース2025年3月号掲載
理学のススメ>

~ 大学院生からのメッセージ~
分野の交差点を照らすムーンシャイン現象

岡田 昌樹Masaki Okada

物理学専攻 博士課程2年生

出身地 福岡県

出身学部 東京大学理学部物理学科

数理科学の発展の歴史では，まったく関係がないと思われていた研究の間に共通点が見つかって，よく調べると実は背後に両者を関係づける深い理論が潜んでいたことが分かり，理解が進展する，ということがたまに起こります。それは数学の分野間で起きたり，物理の分野間で起きたり，ときには数学と物理の間でも起こります。

数学の代数学という分野は，さまざまな計算の構造を抽象化して調べる学問です。計算のことを演算とも言います。例えば整数どうしを足し算した結果は再び整数なので，整数全体の集合には足し算という演算が定まります。このように，性質の良い演算が定義されている集合を群と言います。

整数は無限個ありますが，有限個の要素しかもたない群も存在し，そのような群を有限群と言います。例として，正三角形の対称性の群を挙げます。正三角形は，図の通り，3種類の回転と3種類の鏡映の，計6つの操作のもとで対称です。これらの操作から2つ選んで連続して行うと，結果は6つの操作のどれかと一致します。したがって，正三角形の6つの対称操作は，連続して行うという「演算」のもとで有限群になります。

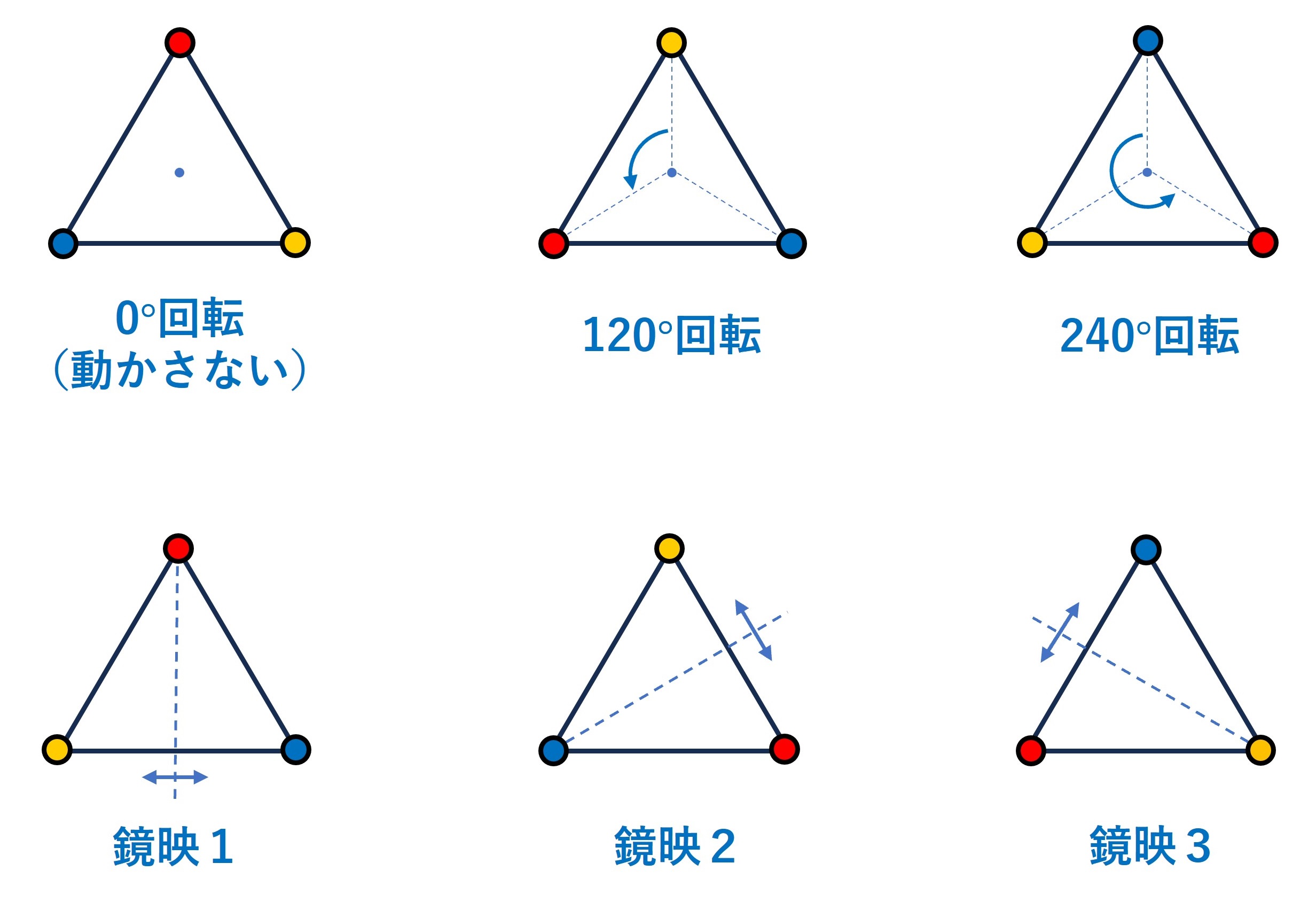
図は，正三角形の6つの対称操作

何かを調べる上で，分解や分類はしばしば有効な手段です。物質が分子や原子に分解できるように，有限群も小さな有限群に分解できることが知られていて，それ以上分解できない基本的な有限群を有限単純群と言います。有限単純群はたくさん存在しますが，多くの数学者の膨大な努力によって，完全な分類の証明が2004年に完了しました。その結果によると，有限単純群は3つの系列と，どの系列にも属さない26個の「その他」に分類されます。「その他」の中で最も大きなものは，約8×10⁵³個もの要素をもつ巨大な群で，モンスター群と呼ばれています。

1978年，ジョン・マッカイ（John McKay）という数学者が，ｊ関数と呼ばれる関数に現れる係数が，なぜかモンスター群の既約表現と呼ばれるものの次元を用いて簡潔に表せることに気づきました。ｊ関数は，有限群論とは全く異なる楕円曲線論という分野で重要な関数だったので，当時の数学者たちはこの事実に驚き，これをムーンシャイン現象と名付けました。英単語のmoonshineには，月光の他に「荒唐無稽な考え」という意味があり，当時はこの事実があまりに突飛で一見「でたらめ」としか思えなかったことを意味しています。

ムーンシャイン現象は，「モンスター群が対称性になっていて，その情報がｊ関数で表されるような『何か』が背後に存在すること」を示唆します。数学者たちは実際に，頂点作用素代数と呼ばれるものを用いて，その「何か」を構成することに成功しました。興味深いことに，頂点作用素代数は，物理の二次元共形場理論という理論を数学的に表したものになっています。数学の分野間の不思議な関係を取り持つ理論は，さらに物理的な解釈をも与えるものになっていたのです。

二次元共形場理論は，物理の弦理論を記述する重要な理論で，盛んに研究されてきました。そして数学と相互作用を起こした結果，モンスター群とｊ関数以外にも，さまざまな有限群と関数の間にムーンシャイン現象が発見されました。その中には，背後にある「何か」がまだ解明されていないものもあります。

二次元共形場理論は，理論物理の中でも特に多様な数学と関連する分野です。理論物理の数理的な側面に興味があった私は，この理論を勉強する中でムーンシャイン現象と出会い，現在その背後にある「何か」に少しでも迫りたいなと研究しています。