Disclaimer: machine translated by DeepL which may contain errors.
The Rigakubu News
The Rigakubu News March 2025
Advancing Science >
~ A Message from a Graduate Student~.
The Moonshine phenomenon, shedding light on the intersections of different fields
 |
| Masaki Okada |
| Department of Physics 2nd Year Doctoral Student |
| Birthplace Fukuoka, Japan |
| Faculty Department of Physics, The University of Tokyo |
In the history of the development of mathematical sciences, it sometimes happens that we find commonalities between researches that were thought to be completely unrelated, and upon closer examination, we discover that there is actually a deep theory behind the relationship between the two, which leads to a better understanding. This sometimes happens between fields of mathematics, sometimes between fields of physics, and sometimes between mathematics and physics.
The field of algebra in mathematics is the study of abstraction and investigation of the structure of various computations. Computations are also called operations. For example, the result of adding integers together is again an integer, so the operation of addition is defined for the whole set of integers. Thus, the set of defined operations with good properties is called a group.
Although there are an infinite number of integers, there are groups with only a finite number of elements, and such groups are called finite groups. As an example, let us take the symmetry group of an equilateral triangle. As shown in the figure, an equilateral triangle is symmetric under three types of rotations and three types of reflections, for a total of six operations. If two of these operations are chosen in succession, the result will coincide with one of the six operations. Thus, the six symmetric operations of an equilateral triangle are a finite group under the "operation" of successive operations.
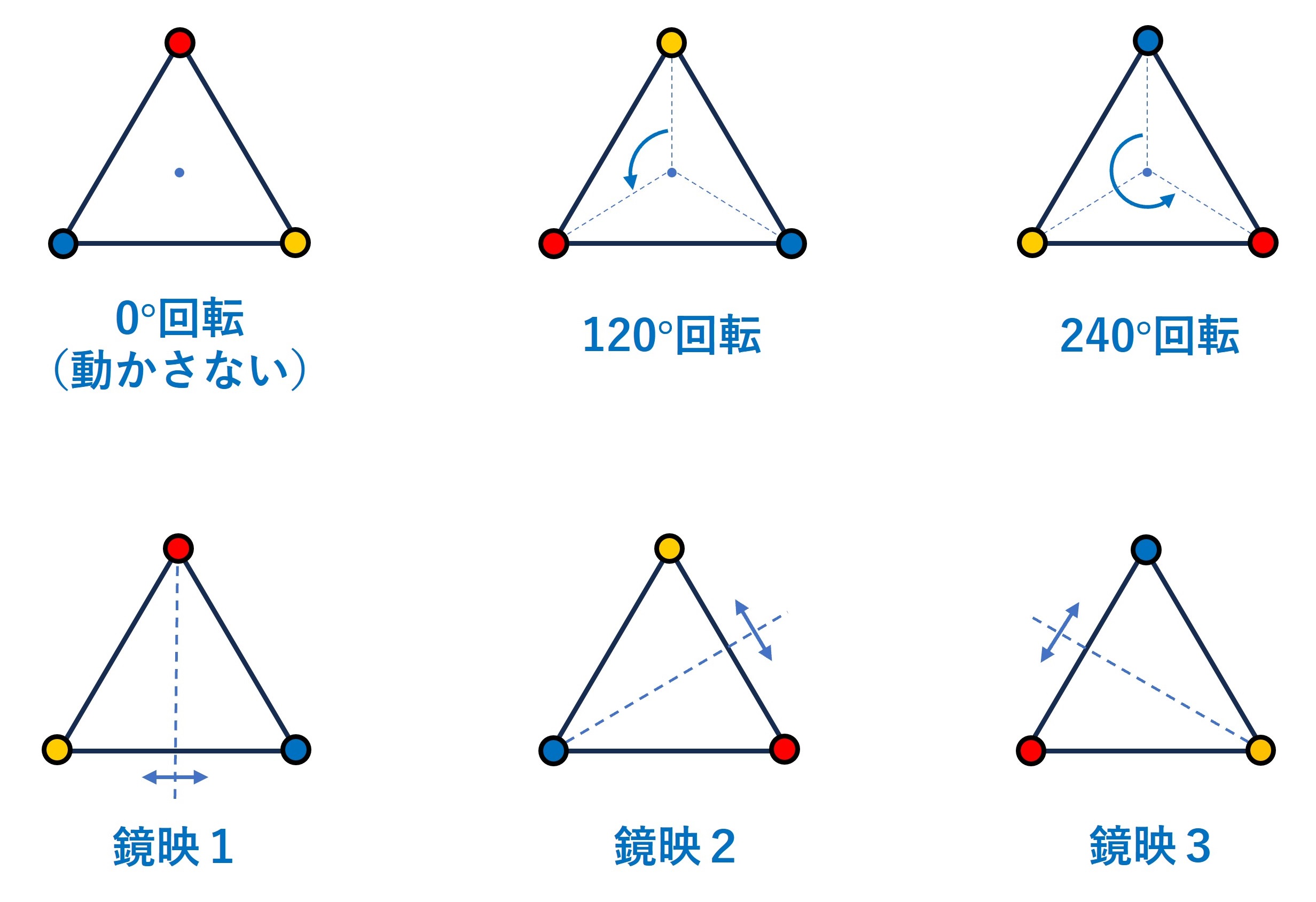
Figure shows the six symmetry operations of an equilateral triangle
Decomposition and classification are often useful tools for studying something. Just as matter can be decomposed into molecules and atoms, finite groups are known to be decomposable into smaller finite groups, and the basic finite groups that cannot be further decomposed are called finite simple groups. Although there are many finite simple groups, the proof of the complete classification was completed in 2004, thanks to the enormous efforts of many mathematicians. According to the results, finite simple groups can be classified into three families and 26 "others" that do not belong to any family. The largest of the "others" is a huge group of about 8 × 1053 elements, called the monster group.
In 1978, a mathematician named John McKay noticed that the coefficients appearing in a function called the j-function could somehow be expressed concisely using the dimension of what is called the irreducible representation of the monster group. j-function was an important function in the field of elliptic curve theory, which is completely different from finite group theory. The mathematicians of the time were so amazed by this fact that they named it the moonshine phenomenon. The English word moonshine means "ridiculous idea" as well as "moonlight," meaning that at the time this fact seemed so far-fetched that it could only be considered "nonsense" at first glance.
The moonshine phenomenon suggests that "there is 'something' behind the monster group such that it is a symmetry and its information is represented by the j-function. Mathematicians have actually succeeded in constructing that "something" using something called vertex operator algebra. Interestingly, vertex operator algebras have become the mathematical expression of a theory of physics called two-dimensional conformal field theory. The theory, which was a curious interrelationship between fields of mathematics, also provided a physical interpretation.
Two-dimensional conformal field theory is an important description of string theory in physics and has been actively studied. As a result of interactions with mathematics, moonshine phenomena have been discovered between various finite groups and functions, in addition to monster groups and j-functions. Some of them have not yet been clarified as to "what" is behind them.
Two-dimensional conformal field theory is an area of theoretical physics that is associated with a wide variety of mathematics. As I was interested in the mathematical aspects of theoretical physics, I encountered moonshine phenomena while studying this theory, and I am now researching them in the hope of finding out "something" behind them.


