~ 大学院生からのメッセージ~
不等式の数学で探る,生命機能の物理的制約
 |
| 大賀 成朗 |
| 物理学専攻 博士課程2年生 |
| 出身地 東京都 |
| 出身高校 東京都立両国高等学校 |
| 出身学部 東京大学理学部 物理学科 |
生命は,外部から栄養を取り入れて生きている。取り入れた栄養は,一部は体を作る材料として固定されるが,残りは体内のいろいろな生命機能——たとえば,物質の合成,輸送,情報伝達,それらの制御——を実現するためのエネルギー(自由エネルギー)として消費される。取り入れる栄養には限りがあるから,生命はそれを各機能に効率よく振り分けているはずだ。その振り分けは,どのような原理に従って,どう決まっているのだろうか? それを探る一つのアプローチが,生物・非生物を問わず全てのものが従う物理的制約を発見することだ。
たとえば,体内時計のように,生体内で規則正しい振動リズムを作る機能を考えよう。生体内の系は非常に小さいため,絶えずふらふらとゆらいでおり,規則正しいリズムを作るには,駆動力(エネルギーを供給する機構)を使ってゆらぎを抑える必要がある。では,駆動力が弱くても,系の構造やしくみをうまく工夫すれば,十分に規則正しい振動を実現できるのだろうか? それとも,物理的制約があって,一定の強さの駆動力で作れる規則正しさには限界があり,それ以上の規則正しさを作るには駆動力を強めるしかないのだろうか。
私が共同研究者と一緒に物理的制約の研究を始めたころ,そうした限界について一つの予想があった。7年前,ドイツの研究グループはコンピューター上でいろいろな小さい化学反応系を調べ,規則正しさが保たれる振動回数——体内時計で言えば,時計が狂い始めるまでに経過する日数——が,駆動力の強さ(ボルツマン定数の何倍かで表す)の4π²分の1を上回れないようだ,と予想したのだ。だが,どんな系を使ってどう工夫してもこの限界を破れない,ということを数学的に証明するのは,未解決の問題だった。
私たちは3週間ほど数式と格闘したのち,この予想の証明に成功した。そこで主に使ったのは,大学1年生で習うコーシー・シュワルツの不等式と,平面図形の等周不等式である。等周不等式は,「周の長さが同じ図形のうちで,面積が最大の図形は円である」ことを不等式の形で表したものだ。それが,一見平面図形と関係ないところで役立つのは面白い。
さらに,ここから思いがけない展開が待っていた。同じ証明手法が,はるかに広い範囲の現象にも適用できたのだ。その結果,これまで予想もされていなかった物理的制約が,数学の力でひとりでに立ち現れた。たとえば,生体内の情報伝達の大きさや,回転する分子機械の回転の強さなども,同じように駆動力の強さに比例する限界をもつことがわかった。
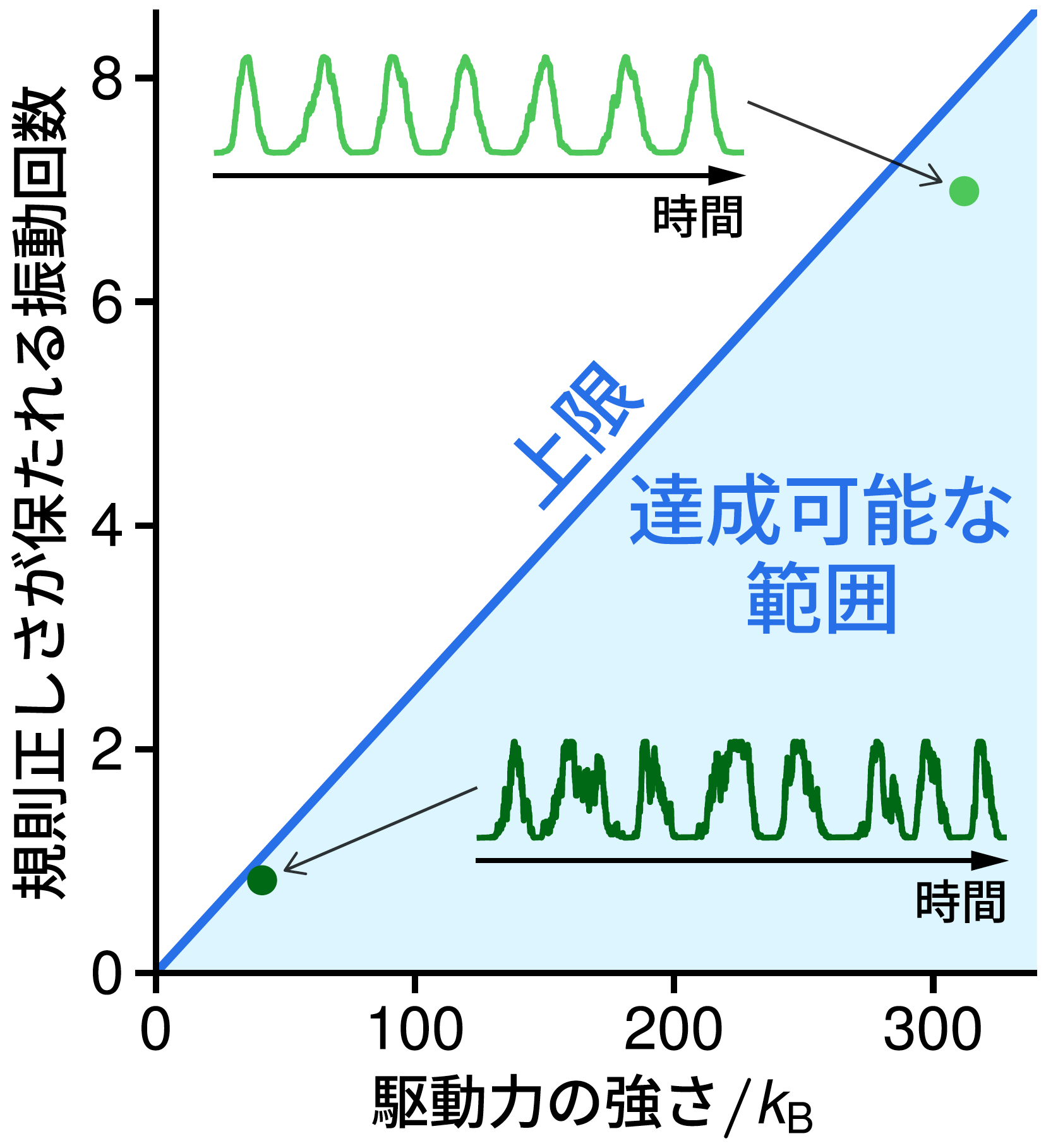
振動リズムの規則正しさについての物理的制約と,振動の実例。
N. Ohga et al., Phys. Rev. Lett. 131, 077101(2023)に基づく
この研究は,非平衡熱力学の分野に属している。非平衡熱力学は,生命を含む身近なスケールの現象を,消費エネルギーの側面から普遍的に理解しようとする物理学だ。そこでは,ある性質が普遍的,つまりどんな構造のどんな系にも成り立つことを示し,その理由を解明するために,数学を用いた論証が活躍する。私は高校生以前から数学が好きだったが,物理を学んでからは,身近なスケールの現象により強い興味を持つようになった。非平衡熱力学はちょうどこの二つの交差点にあって,数学を使って新たな視点を切り拓く面白さにあふれていると思う。


