Disclaimer: machine translated by DeepL which may contain errors.
~ Message from a graduate student~.
Physical Constraints on Biological Functions, Explored by Mathematics of Inequalities
 |
| Department of Physics 2nd Year Doctoral Student |
| Place of birth Tokyo, Japan |
| High School Ryogoku High School, Tokyo |
| Faculty Department of Physics, Faculty of Science, The University of Tokyo |
Life is sustained by nutrients taken in from the outside. Some of the nutrients are fixed as materials to build the body, but the rest is consumed as energy (free energy) to realize various biological functions in the body, such as synthesis of substances, transportation, information transmission, and their control. Since there is a limit to the amount of nutrients that can be taken in, life must allocate them efficiently to each function. How is this allocation determined, and according to what principles? One approach is to discover the physical constraints to which all things, living and nonliving, are subject.
Consider, for example, the function of a regular oscillating rhythm in a living organism, such as a biological clock. The system in a living organism is so small that it is constantly fluctuating, and to create a regular rhythm, it is necessary to suppress the fluctuation by using a driving force (a mechanism to supply energy). Then, even if the driving force is weak, is it possible to achieve sufficiently regular oscillation if the structure and mechanism of the system are well designed? Or is there a physical limit to the regularity that can be achieved with a constant driving force, and the only way to achieve greater regularity is to increase the driving force?
When my collaborators and I started studying physical constraints, we had a prediction about such a limit. 7 years ago, a German research group studied various small chemical reaction systems on a computer and found that the number of oscillations that can be maintained with regularity--the number of days that elapse before the clock goes out of order in the case of a biological clock--is the same as the number of days that can be maintained with regularity in the case of a biological clock. They predicted that the number of oscillations that would maintain regularity-the number of days that would elapse before the clock started going haywire, in the case of a biological clock-would be no greater than 4π² of the strength of the driving force (expressed as a multiple of Boltzmann's constant). But proving mathematically that this limit could not be broken, no matter how ingenious one might be with any system, was an open question.
After three weeks of struggling with the equations, we succeeded in proving this conjecture. We mainly used Cauchy-Schwartz inequalities and isoperimetric inequalities of plane figures, which are taught in the first year of college. The isoperimetric inequality expresses in the form of an inequality that "the figure with the largest area among figures with the same perimeter length is a circle. It is interesting that this inequality is useful in a place seemingly unrelated to plane figures.
Furthermore, an unexpected development awaited us from here. The same proof method could be applied to a much wider range of phenomena. As a result, physical constraints that had never been anticipated before appeared by themselves through the power of mathematics. For example, the magnitude of information transmission in living organisms and the rotational strength of rotating molecular machines were found to have limits proportional to the strength of the driving force.
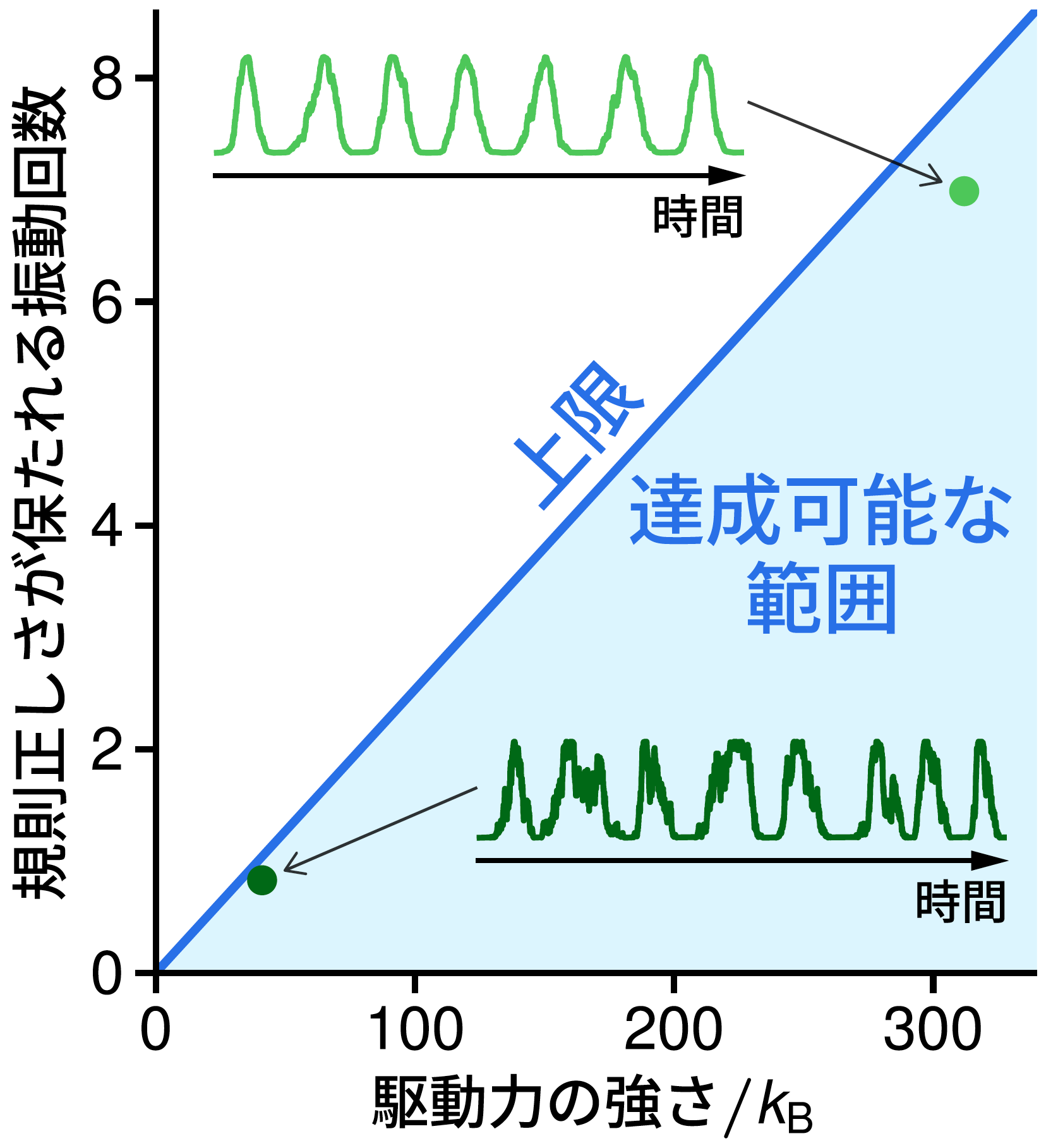
Physical constraints on the regularity of vibrational rhythms and examples of vibrations.
Based on N. Ohga et al., Phys. Rev. Lett. 131, 077101 (2023)
This study belongs to the field of nonequilibrium thermodynamics. Non-equilibrium thermodynamics is a branch of physics that attempts to universally understand phenomena on familiar scales, including life, from the aspect of energy consumption. In this field, mathematical arguments are used to show that certain properties are universal, i.e., they are true for any system with any structure, and to elucidate the reasons why they are true. I liked mathematics even before high school, but after studying physics, I became more interested in phenomena on a familiar scale. Non-equilibrium thermodynamics is just at the intersection of these two, and I think it is full of interesting ways to use mathematics to open up new perspectives.


