DATE2022.10.12 #Press Releases
量子コンピューターによる強レーザー場中の窒素分子イオンの電子波束計算
西 孝哲(化学専攻 特任研究員)
Erik Lötstedt(化学専攻 准教授)
山内 薫(化学専攻 教授)
発表のポイント
- 量子コンピューター実機を用いた強レーザー場中で起こる原子・分子過程の世界初の実証研究。
- 強レーザー場によって駆動される窒素分子イオンの電子波束を、変分量子回路で表現し、その時間発展を計算した。量子コンピューター ibm_kawasakiを用いた。
- 誤り抑制手法として、Cliffordデータリグレッション(CDR)を適用することで、電子波束の時間発展を定性的に再現することに成功した。
発表概要
量子系の時間発展のシミュレーションは、量子計算を適用できる重要な問題の一つである。時間発展のシミュレーションを、最も単純な量子アルゴリズムで行うと、シミュレーション時間の増加とともに量子回路が長くなり、現在利用可能な量子コンピューターではノイズの影響が大きくなり過ぎるため、計算結果を正しく得ることが困難となる。したがって、「如何に効率の良い、短い量子回路を構築するか」という問題と、「その量子回路を用いて計算した結果に含まれるエラーを如何に補正して、より正しい値を予測するか」という問題に指針を与えることが喫緊の課題となっている。
東京大学大学院理学系研究科のLötstedt准教授・山内教授らの研究グループは、東京大学量子イニシアティブにおいて DIC株式会社の支援の下「Qubit による応用量子化学(AQUABIT)」プロジェクト(https://www.u-tokyo.ac.jp/adm/fsi/ja/projects/quantum/project_00064.html)を推進し、「分子系の計算を量子コンピューターによって行うための方法論の開発」と「量子コンピューターによる計算結果の誤り抑制(注1)による計算確度の向上」に取り組んできた。
本研究は、その一環として、強レーザー場によって駆動される窒素分子イオンの電子波束の時間発展を、量子コンピューター ibm_kawasaki(注2)によって計算した。量子回路を少数の変分パラメーターを用いて構成し、変分パラメーターが満たすべき方程式を構築するために必要な期待値の計算を量子コンピューターによって行った。そして、古典コンピューターを用いて効率よく計算することができる特殊な量子回路を用いて、量子コンピューターのノイズによるエラーを見積もり、誤り抑制を行うことによって、時間発展を定性的に再現できることを示した。
なお、本論文は、AVS Quantum Science 誌に発表される論文の中で特に注目すべき論文として Featured Article に選ばれた。
発表内容
窒素分子(N2)に波長800 nmの高強度パルスレーザーを照射すると、電場強度が最大となるパルスのピーク付近の時間においてイオン化が起こり、窒素分子イオン(N2+)が生成される。この窒素分子イオン中の電子は、さらにパルス後半の電場によって駆動され、波長391 nmの二次的なレーザー光を発生することが知られている。この現象を説明するモデルとして、窒素分子イオンの3つの電子状態、X, A, Bを考える。初期状態としてX状態にある電子が、パルス後半の電場によってA状態とB状態にも存在するようになる。3つの状態の占有率の時間変化は図1のようになる。
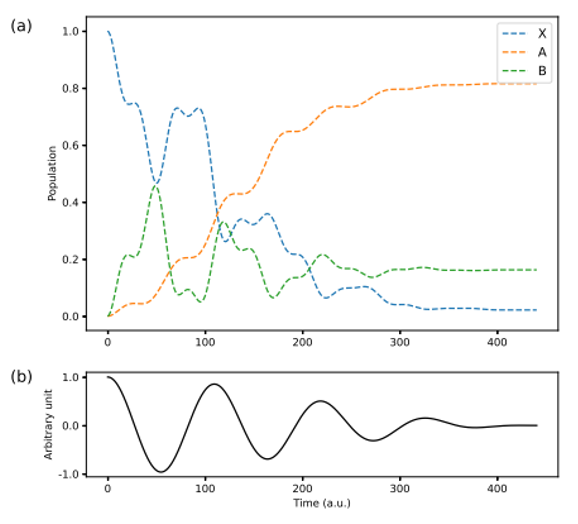
図1:(a)窒素分子イオンの3つの電子状態の占有率の時間変化、(b)パルス後半の電場。
ここで、(b)はパルス後半の電場を示している。(a)から、X状態の占有率が低下していき、最終的には占有率の大きい方から、A状態、B状態、X状態の順になることがわかる。特に、B状態がX状態より多く占有されることで、391 nmの二次的レーザー光が放出される。 このような時間発展は、時間依存シュレーディンガー方程式の解 ![]() として得られる。任意の時刻における解を短い量子回路で表現するために、変分量子回路
として得られる。任意の時刻における解を短い量子回路で表現するために、変分量子回路![]() (注3)を初期状態
(注3)を初期状態 ![]() に作用させ、
に作用させ、![]() を仮定すると、変分パラメーターの時間微分
を仮定すると、変分パラメーターの時間微分![]() が従うべき方程式は
が従うべき方程式は ![]() で与えられる。M,V は、以下のように定義される。
で与えられる。M,V は、以下のように定義される。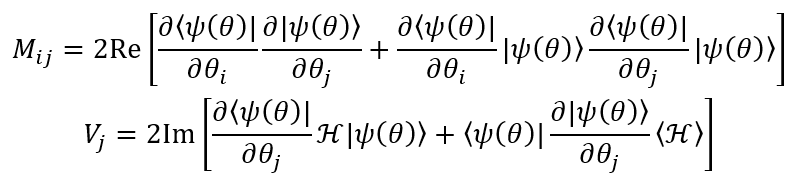
ここで、![]() はハミルトニアン。このように M,V を量子コンピューターで計算し、
はハミルトニアン。このように M,V を量子コンピューターで計算し、![]() を古典コンピューターで解く手法は、変分量子シミュレーター法と呼ばれる。本研究では
を古典コンピューターで解く手法は、変分量子シミュレーター法と呼ばれる。本研究では ![]() を4つのパラメーターによって表現することで、
を4つのパラメーターによって表現することで、![]() を効率よく近似できることを示した。 実際に量子コンピューターで M と V を計算するには、補助量子ビットを用いた量子回路を実行する必要があるが、ibm_kawasakiのように量子ビット間の結合が限られている場合には量子回路が長くなり、ノイズを増加させてしまう。このため、適切な誤り抑制を行わない限り正しい計算ができない。本研究では、CDRと呼ばれる誤り抑制法を適用した。
を効率よく近似できることを示した。 実際に量子コンピューターで M と V を計算するには、補助量子ビットを用いた量子回路を実行する必要があるが、ibm_kawasakiのように量子ビット間の結合が限られている場合には量子回路が長くなり、ノイズを増加させてしまう。このため、適切な誤り抑制を行わない限り正しい計算ができない。本研究では、CDRと呼ばれる誤り抑制法を適用した。
万能量子計算をするには、Cliffordゲートと非Cliffordゲートと呼ばれる2種類の量子ゲート(注4)が必要であることが知られている。このうち、量子回路に含まれる非Cliffordゲートの数が少ない場合、古典コンピューターを用いて効率よく量子回路をシミュレーションできる。そこで、実行したい量子回路の非Cliffordゲートの一部をCliffordゲートで置き換えた量子回路を、量子コンピューターと古典コンピューターの両方でシミュレーションし、結果を比較することによって、量子コンピューターでの計算における計算誤りの大きさを見積もることができる。この見積もりを元に、本来の非Cliffordゲートを多く含んだ量子回路の計算誤りを抑制する方法をCDRと呼ぶ。
図2にibm_kawasakiを用いたシミュレーション結果を示す。
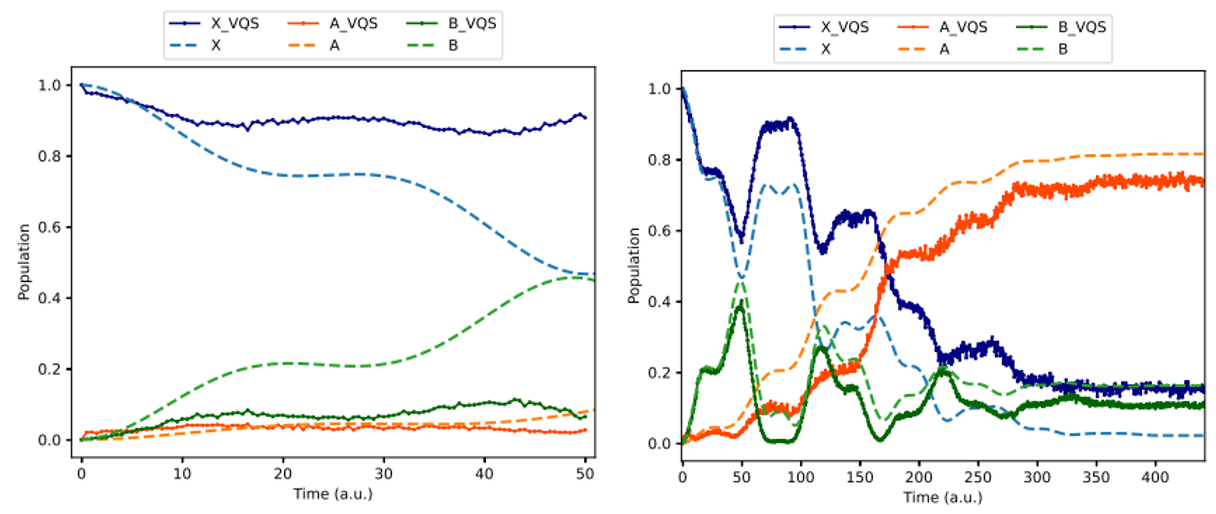
図2:ibm_kawasakiを用いたシミュレーション結果。正確な解は点線、ibm_kawasakiを用いて得られた結果は実線。左はCDRを適用せずに計算した100ステップ、右はCDRを適用して計算した882ステップの時間発展。
図2内の左図のように、CDRを適用しなかった場合(実線)、正しい時間発展(点線)を再現できない。一方、右図のように、CDRを適用し、補助量子ビットを用いた量子回路の誤りを抑制することによって、定性的に時間発展を再現できている。CDRを適用する際に、非Cliffordゲートを置き換えるCliffordゲートの選び方にはある程度の自由度があるが、本研究では、置き換えたい非Cliffordゲートに最も類似したCliffordゲートのみを採用することによって、量子コンピューターを用いる回数を減らし、効率よくCDRを実行できることを示した。
発表雑誌
-
雑誌名 AVS Quantum Science 論文タイトル Simulation of a laser-driven three-level system by a noisy quantum computer 著者 Takanori Nishi, Erik Lötstedt, Kaoru Yamanouchi DOI番号
用語解説
注1 誤り抑制
量子回路の実行結果に含まれる計算エラーを軽減する手法。古典コンピューターで効率良くシミュレーション可能な量子回路の結果と比較することによって結果を改善するCDRの他、ノイズの大きさを変化させることによってノイズと計算エラーの関係を調べ、ノイズがゼロの場合を推測する、zero noise extrapolationと呼ばれる手法が知られている。↑
注2 量子コンピューター ibm_kawasaki
量子ビットと呼ばれる2準位系を用いて、 |0⟩ と |1⟩ の量子状態を情報の単位とするコンピューター。1950年代にアイディアが提案され2000年ごろから小規模なものが作られている。近年では、IBM、IonQなどによって研究利用可能な量子コンピューターが現れており近い将来の実用化が期待されている。ibm_kawasakiは昨年2021年東京大学に導入された27量子ビットを持つ超伝導量子回路型量子コンピューターである。↑
注3 変分量子回路
変分パラメーターを用いて構成された量子回路。量子回路に用いる量子ゲートの種類と順序は固定し、変分パラメーターのみを最適化することで量子計算を実行する。本研究では変分パラメーターの最適化を
を解くことによって行った。↑
注4 量子ゲート
量子コンピューターにおける論理演算の単位。Pauli演算子のテンソル積の集合 S の要素 σ に対して、
となるものをCliffordゲート、それ以外を非Cliffordゲートと呼ぶ。↑


