DATE2023.12.05 #Press Releases
超伝導型量子コンピューター vs. イオントラップ型量子コンピューター
――スピンダイナミクスをどちらがより速く、より正確に解けるか?――
エリック・ローツステット(化学専攻 准教授)
山内 薫(アト秒レーザー科学研究機構 特任教授)
発表のポイント
- 超伝導型量子コンピューター(ibm_prague)とイオントラップ型量子コンピューター(Quantinuum H1-1) のパフォーマンスを一次元Heisenbergスピン系の時間発展をシミュレーションすることにより比較した。
- どちらの量子コンピューターを用いても、スピン系のダイナミクスが正確にシミュレーションされた。両方式の量子コンピューターはともに将来も有望な量子デバイスである。
- ibm_prague の場合には誤り抑制が必要となるが、Quantinuum H1-1の場合には誤り抑制は不要であった。一方、Quantinuum H1-1を用いた場合の計算には、ibm_pragueを用いた場合に比べて約200倍の時間がかかった。
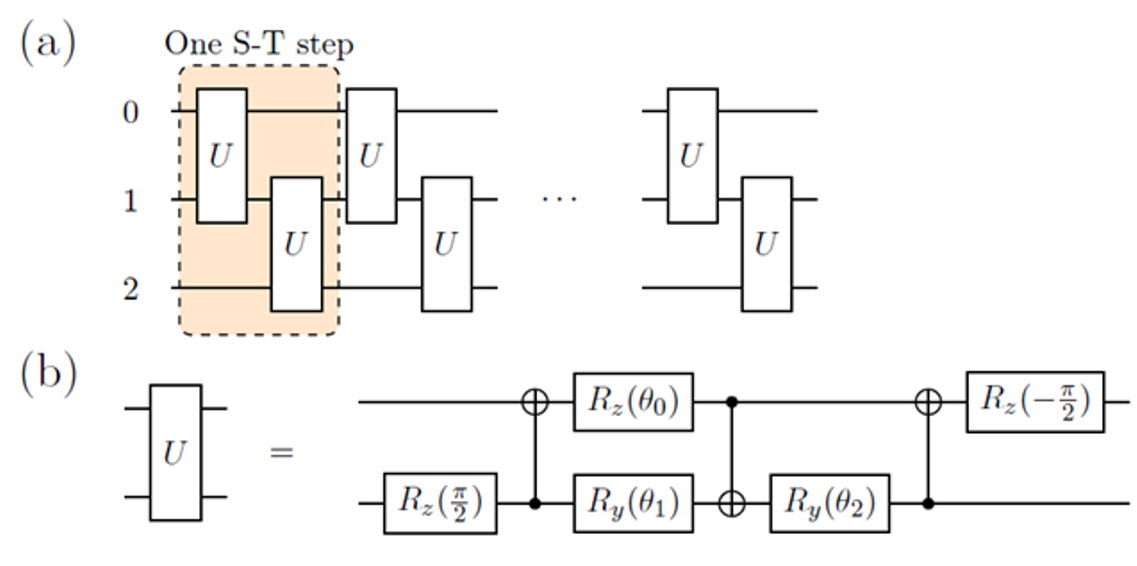
Heisenberg スピン系をシミュレーションするための量子回路
概要
東京大学大学院理学系研究科のエリック・ローツステット准教授と、アト秒レーザー科学研究機構の山内 薫特任教授らによる研究グループは、スピン系の時間発展のシミュレーションを通じて、超伝導型量子コンピューター(注1)とイオントラップ型量子コンピューター(注2)のパフォーマンスを比較し、それぞれの特性を明らかにした。 近年の量子コンピューター(注3)の技術発展には目覚ましいものがあり、量子コンピューターの性能も年を追うことに向上している。それだけに、量子コンピューターを基礎・応用研究に利用する際には、最新の量子コンピューターがどのようなパフォーマンスを持つかを十分に把握しておく必要がある。本研究グループは、超伝導型量子コンピューターとしてIBM社が開発した量子コンピューターの最新機種であるibm_prague (Heronプロセッサのプロトタイプを搭載)を、イオントラップ型量子コンピューターとしてQuantinuum 社の最新機種の一つである H1-1 を用い、3つのスピンからなる最も基本的なHeisenberg スピン系(注4)の時間発展を計算し、その結果を比較した。その結果、どちらの量子コンピューターを用いても、スピン系のダイナミクスが正確にシミュレーションされた。このことから、両方式の量子コンピューターがともに将来も有望な量子デバイスであることが示された。また、ibm_prague の場合には、3種類のエラー抑制(注5)が必要であったが、Quantinuum H1-1の場合にはエラー抑制は不要であった。一方、Quantinuum H1-1を用いた場合の計算時間は、ibm_pragueを用いた場合の計算時間に比べて約200倍となることが示された。
発表内容
【研究の背景】
現在利用できる量子コンピューターはNISQデバイス(注6)と呼ばれるもので、環境との相互作用から生じる多くの種類のノイズのために量子演算にエラーが生じてしまう。そのため、量子コンピューターで実行された計算結果から、意味のある結果を抽出するためには、ノイズの影響を減らす誤り抑制を行うことが必要である。
一方、近年の量子コンピューターの技術発展には目覚ましいものがあり、量子コンピューターの性能も年を追うことに向上している。なかでも、超伝導型量子コンピューターとイオントラップ型量子コンピューターについては、ユーザーのためのプラットフォームが用意されており、それらの性能や特徴を生かした量子アルゴリズムの開発が進められている。ところが、現時点では、超伝導型量子コンピューターとイオントラップ型量子コンピューターの性能がどのように異なるのかを具体例のシミュレーションを基に比較した例は知られていない。そのため、これらの別々の方式の量子コンピューターを用いて、共通の問題を解き、そのパフォーマンスを比較することが待ち望まれていた。
【研究内容】
超伝導型量子コンピューターとして、IBM社が開発した量子コンピューターの最新機種であるibm_prague (Heronプロセッサのプロトタイプを搭載)を、イオントラップ型量子コンピューターとして、Quantinuum 社の最新機種の一つである H1-1 を用い、最も基本的な1次元3サイトHeisenberg スピン系のダイナミクスを計算し、その結果を比較することを通じて、これからの量子コンピューターを活用した基礎・応用研究への指針を与えることを試みた。
シミュレーションでは、3 つの量子ビットを使用し、Suzuki-Trotter近似(注7)を使用して、時間依存ダイナミクスの量子計算を行った。シミュレーションで使用された量子回路を図 1 に示す。

図1:Heisenberg スピン系をシミュレーションするための量子回路。
8個のSuzuki-Trotter ステップから構成されている。
シミュレーションの結果を図 2に示す。図 2(右)に示されているように、ibm_pragueの場合には、ダイナミック・デカップリング(DD) 、パウリ・トワーリング(PT)、読み出しエラーの抑制(M3)という3つのエラー抑制を行った上でスピンを保存しない状態を除去して波動関数を正規化した結果赤い曲線が得られ、古典コンピューター(注8)で得られた正しい曲線(黒い曲線)をほぼ完全に再現した。また、図2(左)に示されているように、Quantinuum H1-1 の場合には、得られた結果そのままで古典コンピューターによって得られた正しい曲線(黒い曲線)をほぼ再現しており、スピンを保存しない状態を除去して波動関数を正規化しただけで赤い曲線が得られ、正しい曲線をほぼ完全に再現した。
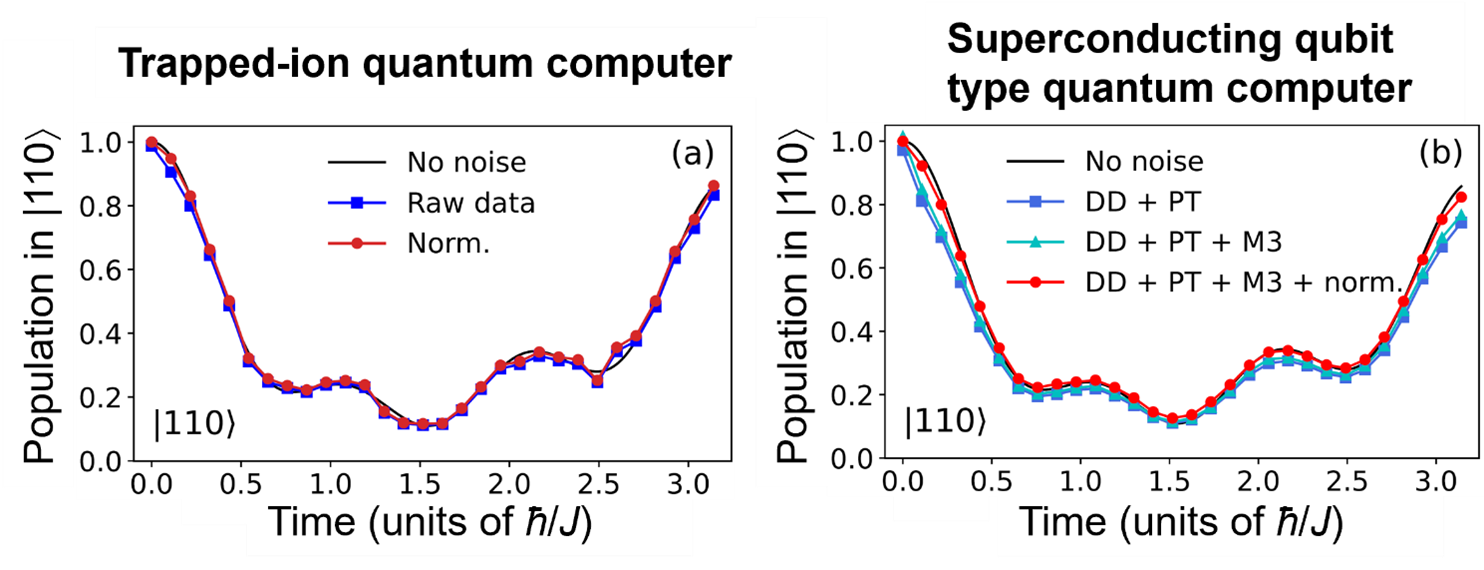 図2:量子ビット状態 |110> の分布の時間発展
図2:量子ビット状態 |110> の分布の時間発展
(a) イオントラップ型量子コンピューター Quantinuum H1-1による結果。 (b) 超伝導型量子コンピューター ibm_prague による結果。3種のエラー抑制手法(DD = Dynamical decoupling, PT = Pauli twirling, M3 = Read-out error mitigation)が用いられている。
一方、Quantinuum H1-1の場合は、データ点ごとに 1024 回の測定を行い、各測定には約 225 ミリ秒かかったが、ibm_prague の場合には、データ点ごとに50048回の測定を行い、各測定に約1ミリ秒かかった。各測定にかかる時間は、Quantinuum H1-1が ibm_prague に比べて約200倍の時間がかかることになる。また、データ点1つごとにかかった時間は、Quantinuum H1-1の場合には 230秒であったのに対して、ibm_prague の場合には 50 秒であった。
【社会的意義・今後の見通し】
超伝導型量子コンピューターおよびイオントラップ型量子コンピューターのそれぞれのハイエンドマシンを用いて量子スピンダイナミクスのシミュレーションを行ったところ、両方式の量子コンピューターともに量子ダイナミクスを正確にシミュレーションできるレベルにあることが示された。さらに、超伝導型量子コンピューターを用いた場合はエラー抑制が必要となるが計算速度が速いという特徴を持つこと、イオントラップ型量子コンピューターを用いた場合は計算の精度が非常に高いものの計算速度が遅いという特徴を持つことが示された。
将来、量子コンピューターのハードウエア開発はますます進歩し、NISQデバイスの性能はますます高くなり、より大きくて複雑なシステムを計算するために量子コンピューターが活用されていくものと予想される。本論文の成果は、そのような場合において、それぞれのNISQデバイスの性能やパフォーマンスに応じて、最適なエラー抑制の方法を開発し適用していくことが重要であることを示しており、誤り耐性量子コンピューター(注9)が確立するまでの間、どのようにNISQデバイスを基礎・応用研究に活用していくかという問題に指針を与えるものである。
〇関連情報:
「量子コンピューターによる強レーザー場中の窒素分子イオンの電子波束計算」(2022/10/12)
「量子コンピューターでのCO2の振動エネルギー準位の計算」(2022/7/14)
「量子コンピューターによるヒュッケル分子軌道計算」(2022/5/13)
論文情報
-
雑誌名 Chemical Physics Letters 論文タイトル Comparison of current quantum devices for quantum computing of Heisenberg spin chain dynamics著者 Erik Lötstedt*, Kaoru Yamanouchi*DOI番号
研究助成
本研究は、東京大学量子イニシアティブプロジェクト「Qubitsによる応用量子化学」を通じたDIC社の支援を受けて、また、IBM社、Quantinuum 社の協力を得て実施された。
用語解説
注1 超伝導型量子コンピューター
このタイプの量子コンピューターでは、量子ビットはミリケルビン温度まで冷却された超伝導回路として実現される。量子ビットはマイクロ波共振器に結合されており、量子ビットの量子状態はマイクロ波パルスによって制御される。 2021年に新川崎に設置された量子コンピューターibm_kawasakiや本論文で用いた ibm_pragueもこのタイプである。↑
注2 イオントラップ型量子コンピューター
このタイプの量子コンピューターでは、量子ビットは、高周波電場によってトラップされたイッテルビウム原子イオンやカルシウム原子イオンなどの原子イオンを用いて実現される。1つのイオン内の2つの電子状態が1量子ビットを表し、量子ビットの状態は、特定の波長を持つレーザー光をイオンに照射することによって操作される。↑
注3 量子コンピューター
量子ビットから構築されているコンピューター。ビットの値が0か1だけをとる古典コンピューターとは異なり、量子ビットは0と1の重ね合わせ状態をとることができる。量子ビット状態の重ね合わせを利用することで、従来の古典コンピューターよりもはるかに大きな分子のシミュレーションが可能になることが期待されている。↑
注4 Heisenbergスピン系
さまざまな材料のスピンダイナミクスを記述するための基本モデル。その状態を量子コンピューター上で直接表現できる。1つの量子ビットは1つのスピンサイトを表し、量子ビットの2つの状態、つまり、状態 0 と 1 はスピン状態の「アップ」と「ダウン」を表す。3サイトのスピン鎖のシミュレーションは古典コンピューターを用いて容易に実行できるが、50サイトを超える大規模なスピン系のシミュレーションについてはスーパーコンピューターを使用しても困難である。そのため量子コンピューターを用いて多数のサイトを持つスピン鎖の計算を示すことは、量子コンピューターの性能を判断する目安となる。↑
注5 エラー抑制
現在利用可能な量子コンピューターによる演算は、量子ビットのデコヒーレンスや量子ビットの状態を制御するために使用されるゲート操作のキャリブレーションなど、さまざまな原因からのノイズの影響を受ける。そのため、意味のある結果を得るには、エラー抑制の手法を用いてエラーの影響を軽減する必要がある。↑
注6 NISQデバイス
Noisy Intermediate-Scale Quantum Computerを指す。ノイズの影響がある中規模の量子コンピューターのこと。現在利用可能な量子コンピューターは皆NISQデバイスである。↑
注7 Suzuki-Trotter 近似
演算子の和を指数部に持つ演算子を各々の演算子の指数演算子の積に分解する近似。量子系の時間発展の計算などに用いられる。↑
注8 古典コンピューター
PC、スーパーコンピューター、スマートフォンなどの従来から存在するコンピューター。↑
注9 誤り耐性量子コンピューター
量子計算において誤りがあっても、その誤りを訂正できるように量子回路を組んだ量子コンピューター↑


