量子コンピューターによるCO2の振動エネルギーの計算る
Lötstedt Erik(化学専攻 准教授)
山内 薫(化学専攻 教授)

![]()
我々は,温室効果ガスとしても知られている三原子分子 CO2の振動準位エネルギーを計算するために,変分量子固有ソルバー(variational quantum eigensolver: VQE)法4)を採用した。VQE では,変分パラメーターに依存する波動関数を量子コンピューター上で記述し,古典コンピューターを用いた最適化アルゴリズムによって変分パラメーターを最適化させ,エネルギーが最小値となるようにエネルギーの近似値を得る。すなわち,量子コンピューターと古典コンピューターの両方を使うハイブリッド方式によって最適エネルギーを求めた。
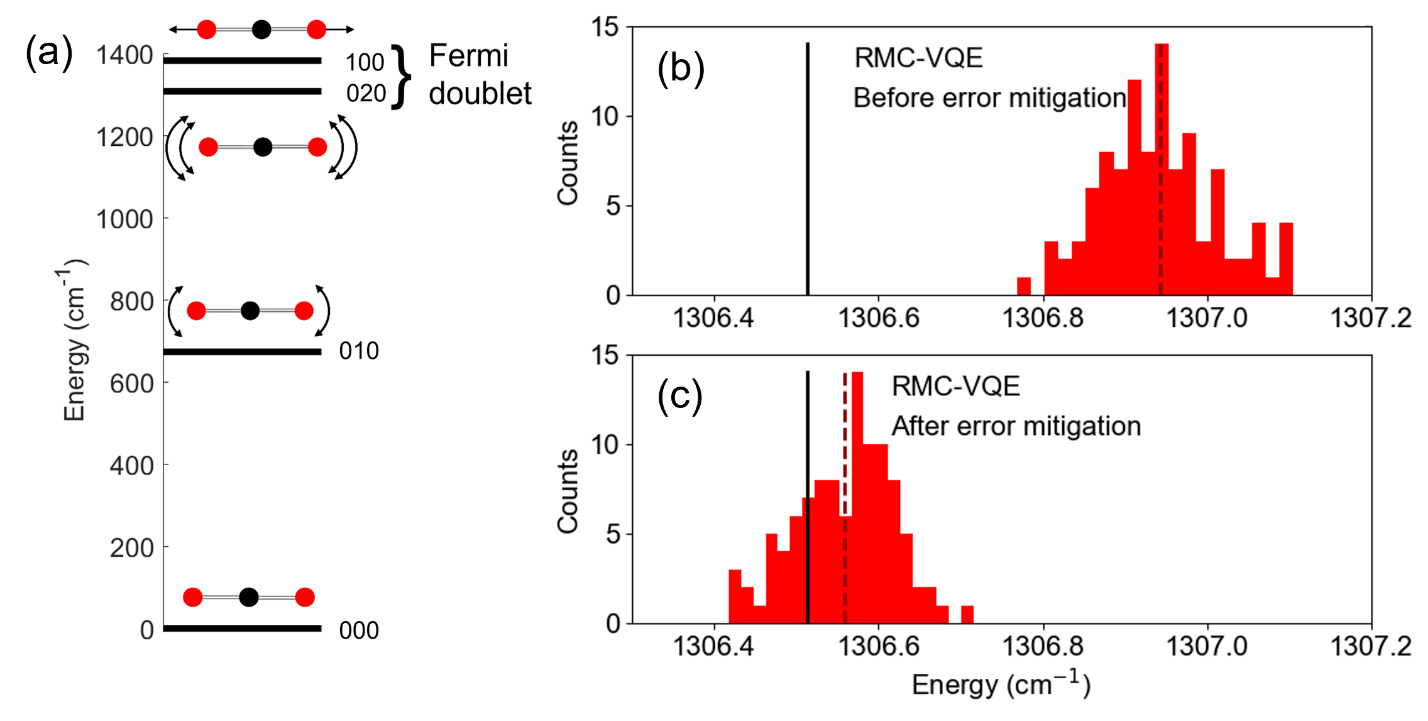
図(b,c)に量子計算によって得られた CO2のFermi 二重項のうちのエネルギーの低い方の準位のエネルギーを示す。これは,VQE 法を改良した縮小多準位縮約変分量子固有ソルバー(reduced multistate contracted variational quantum eigensolver:RMC-VQE)と呼ばれる方法3)によって得られたものである。この RMC-VQE では,必要となる行列要素のみを量子コンピューターによって求め,それ以外の行列要素を古典コンピューターで求めている。このような方式をとるのは,現時点で利用可能な量子コンピューターを用いる場合,さまざまな種類のノイズのために量子演算の結果にエラーが含まれてしまうため,そのエラーの影響を軽減するためである。そして,量子コンピューターを用いて評価された行列要素の値についてはエラーを適切に補正する必要がある。
図(b,c)に示したヒストグラムは,Hamiltonian 行列を 100 回計算し,その都度,対角化して得られた結果を示したものである。行列要素の計算においては,それぞれの量子回路を 8192 回実行し,その平均値を求めている。この図に示されているように,RMC-VQE 法によって得られた準位エネルギーの平均値は,エラー補正の前でも,古典コンピューターで求めたエラーの影響を含まない計算値からの隔たりは約 0.2 cm−1と小さく,エラー補正後は,隔たりはさらに小さく約 0.05 cm−1となっている。このことは,RMC-VQE 法を用いた上でエラー補正を適切に行えば,量子コンピューターによって,CO2分子の振動準位のエネルギーを高い精度で求められることを示している。
本研究では,分子の電子状態の計算5)だけでなく,分子の振動状態の計算においても,量子計算が将来役立つ手法となることを示している。今後,よりサイズの大きな多原子分子の振動準位の計算に、量子コンピューターが活用されていくと期待される。
 |
|
| 図:(a) CO2の振動エネルギー準位。(b,c) Fermi 二重項のうちの低い方の準位のエネルギーのヒストグラム。RMC-VQE 法によって得られたエラー補正無しの場合(b)と有りの場合(c)を比較している。垂直の実線は,古典コンピューターを用いて得られた準位エネルギーの厳密解を表す。垂直の破線は,RMC-VQE 法によって得られた準位エネルギーの平均値を表す | |
本研究はErik Lötstedt et al., AVS Quantum Science 4, 036801(2022)に掲載された。
* 1) IBM Quantum team, https://quantum-computing.ibm.com, 2021, ibm_kawasaki v1.3.20,2) E. Lötstedt, K. Yamanouchi, T. Tsuchiya, and Y. Tachikawa, Phys. Rev. A103, 062609 (2021),3) E. Lötstedt, K. Yamanouchi, and Y. Tachikawa, AVS Quantum Science 4, 036801 (2022),4) A. Peruzzo et al., Nat. Commun. 5, 4213 (2014),5) R. Yoshida, E. Lötstedt, and K. Yamanouchi, J. Chem. Phys. 156, 184117 (2022).


