DATE2022.05.13 #Press Releases
量子コンピューターによるヒュッケル分子軌道計算
吉田 龍平(化学専攻 修士課程1年)
Erik Lötstedt(化学専攻 准教授)
山内 薫 (化学専攻 教授)
発表のポイント
- ヒュッケル分子軌道(注1) ハミルトニアンの行列要素を量子ゲート(注2) を用いて表すことによって、エチレンやベンゼンなどの基本的なπ電子系分子の分子軌道の軌道エネルギーを、量子コンピューターibm_kawasaki(注3) を用いて計算した。
- 量子計算のエラーに伴って生成する物理的に意味を持たない状態を捨てるという最も単純なエラー抑制(注4)の手法を取り入れることによって、軌道エネルギーを高い確度、かつ、高い精度で求めることができることを示した。
- 開発した手法は極めて一般的であるため、フーラレン、グラフェン、カーボンナノチューブなどの大きなπ共役系の電子状態を瞬時にして量子コンピューターによって求めるための指針を与えた。
発表概要
量子コンピューターによる計算が現実のものとなりつつある今、「量子演算において現時点では不可避となっているエラーの発生を如何に抑えるか」というハードウェア面での量子技術開発が重要であることは言うまでもない。しかし、その一方で、「対象となる系の計算を行うために、如何に効率の良い量子回路を構築するか」という問題と、「その量子回路を用いて計算した結果に含まれるエラーを如何に補正して、より正しい値を予測するか」という問題に指針を与えることが喫緊の課題となっている。
東京大学大学院理学系研究科のLötstedt准教授、山内教授らの研究グループは、東京大学量子イニシアティブにおいて DIC株式会社の支援の下「Qubit による応用量子化学 (AQUABIT)」プロジェクト(https://www.utokyo.ac.jp/adm/fsi/ja/projects/quantum/project_00064.html)を推進し、「分子系の計算を量子コンピューターによって行うための方法論の開発」と「量子コンピューターによる計算結果の誤り抑制による計算確度の向上」に取り組んできた。
本研究では、その一環として、最も基本的な分子の電子状態の計算手法であるヒュッケル分子軌道法による分子軌道の計算を、エチレン、シクロプロペン、シクロブタジエン、1,3-ブタジエン、ベンゼンについて、量子コンピューター ibm_kawasaki によって行った。そして、量子計算のエラーに伴って生成する「物理的に意味を持たない状態を」捨てるという最も単純な誤り抑制を行なえば、高い確度、かつ、高い精度で軌道エネルギーを求めることができることを示した。
本研究にて示した「軌道関数の基底関数による展開」および「ハミルトニアン行列の量子回路による記述」はいずれも汎用性があり、今後、フーラレン、グラフェン、カーボンナノチューブなどの大きなπ共役系の電子状態の量子計算に本研究の成果が活用されると予想される。
発表内容
ヒュッケル分子軌道法によるハミルトニアンはパウリ演算子を用いて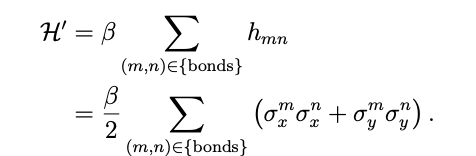
と書ける。ここで、βは共鳴積分、m,nは炭素原子の番号を表現しており、![]() はともにパウリ演算子でそれぞれi番目、j番目の量子ビットに作用していることを示している。
はともにパウリ演算子でそれぞれi番目、j番目の量子ビットに作用していることを示している。
そこで、量子コンピューターによって効率的に計算を行うために演算子Urを導入することによって、ハミルトニアンを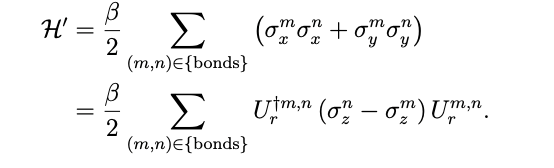
と表す。
このとき、k番目に励起した軌道のエネルギーは、π結合ごとのエネルギーを求めそれを加えて行く形で、k番目の基底関数とそれを軌道に変換する励起演算子![]() を用いて
を用いて
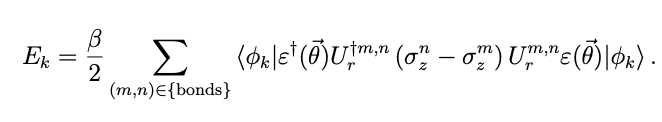
と書ける。このように、すべて軌道エネルギーを CNOTゲートの数が最小となる形で量子ゲートを用いて記述すること可能となった。
例えば、(図1)(c)のシクロブタジエン(C4H4)における炭素原子0番と1番の部分のπ結合における基底状態のエネルギーを求める量子回路は、次項のように表わされる。
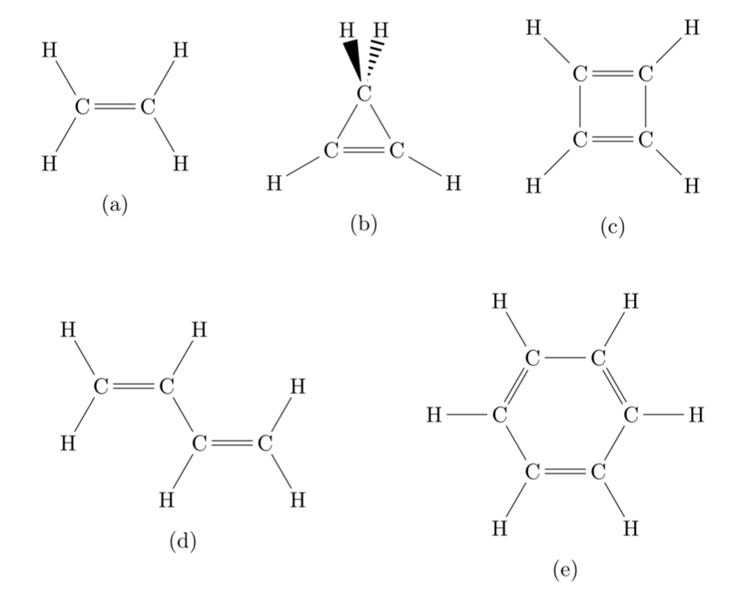
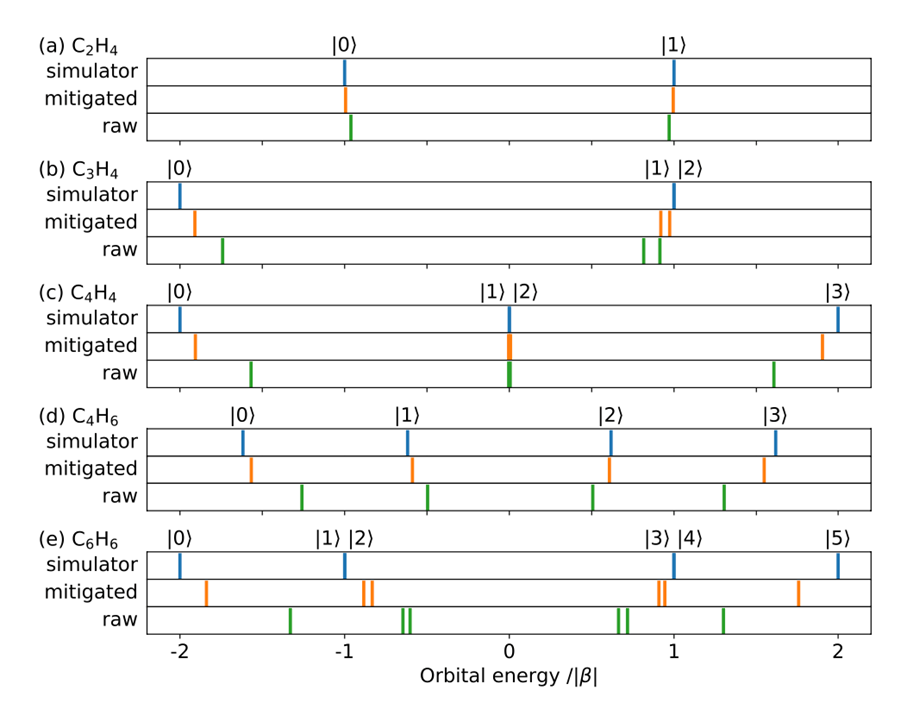
図1:量子コンピューターibm_kawasakiによって軌道エネルギーを求めた5種類のπ電子系分子
(a) エチレン (ethylene) C2H4
(b) シクロプロペン (cyclopropane) C3H4
(c) シクロブタジエン (cyclobutadiene) C4H4
(d) 1,3-ブダジエン (1,3-butadiene) C4H6
(e) ベンゼン (benzene) C6H6
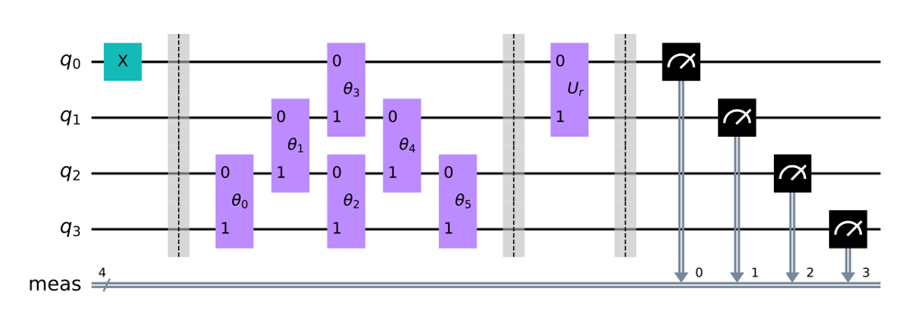
ここで、それぞれの縦長の長方形は演算を意味しており、3本の縦の点線は量子回路の意味を明らかにするための便宜的なものである。最も左の縦の点線の左側では基底関数が用意され、左から1番目と2番目の点線の間は励起演算子による演算を表わしており、そして左から2番目と3番目の点線の間はUrによる演算を表現している。
このような量子回路を量子コンピューターによって計算し、その結果を、古典コンピューターを用いて整理した。実際、上記の様に導入した量子回路では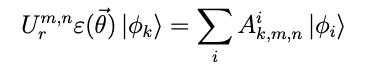
と表わされる振幅![]() の絶対値の二乗を、観測を通じて得ることができる。このとき、軌道エネルギーは、
の絶対値の二乗を、観測を通じて得ることができる。このとき、軌道エネルギーは、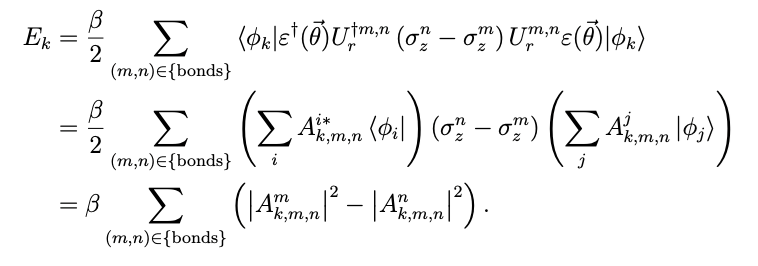
のように、![]() の絶対値の二乗を用いて与えられる。
の絶対値の二乗を用いて与えられる。
そこで、量子コンピューターによってそれぞれの結合毎に計算された|![]() |を用いて、その足し算と引き算のみの処理を古典コンピューターで行うことによって、分子軌道のエネルギーを求めた。
|を用いて、その足し算と引き算のみの処理を古典コンピューターで行うことによって、分子軌道のエネルギーを求めた。
(図1)の5種類のπ電子系分子について、ibm_kawasakiを用いて計算した軌道エネルギーを以下の図の raw の行に示す。比較のために統計誤差も量子コンピューターによる誤差も含まない厳密な解と同じであるシミュレーターの値を simulator の行に示した。
さらに、ibm_kawasakiで計算したのち誤り抑制をした場合の結果を mitigated の行に示した。誤り抑制をすると、計算結果が大きく改善されることが示された。例えば、ベンゼンの基底エネルギーについては、誤り抑制をしない場合α-1.3|β|となり、正しい値α-2 |β|との隔たりが大きいが、ibm_kawasakiを用いて誤り抑制を行うことによってα-1.8|β|と求められ、正しい値により近い軌道エネルギーを求めることができることが示された。
発表雑誌
-
雑誌名 The Journal of Chemical Physics 論文タイトル Quantum computing of Hückel molecular orbitals of π-electron systems 著者 Ryuhei Yoshida, Erik Lötstedt, Kaoru Yamanouchi* DOI番号
用語解説
注1 ヒュッケル分子軌道
1930年にヒュッケルによって提案された分子軌道法。π共役系分子の分子軌道およびそのエネルギーを記述できる。分子軌道を炭素原子の原子軌道の重ね合わせとし炭素原子一つにつき一つのp軌道のみを考慮している。またクーロン積分と共鳴積分の値はそれぞれα,βとして分子内で同じ値と仮定する。 ↑
注2 量子ゲート
古典コンピューターにおけるAND、OR、XOR、NOTゲートなどに対応する量子コンピューターにおける演算の最小単位。一つの量子ビットのみに作用するものを1量子ビットゲート、二つの量子ビットに作用するものは2量子ビットゲートと呼ばれている。超伝導量子コンピューターを含め多くのタイプの量子コンピューターにおいて2量子ビットゲートは1量子ビットゲートより圧倒的にノイズが多いことが知られている。 ↑
注3 量子コンピューター ibm_kawasaki
量子力学に基づき量子状態と呼ばれる0と1の計算基底の重ね合わせを用いて計算を行うコンピューター。1950年代にアイディアが提案され2000年ごろから小さなものが作られている。近年ではDwaveに始まり、IBM、IonQなどによって研究利用可能な量子コンピューターが現れており近い将来の実用化が期待されている。ibm_kawasakiは昨年2021年東京大学に導入された27量子ビットを持つ超伝導量子コンピューターである。↑
注4 エラー抑制
量子ゲートの演算におけるエラーを修正する手法。物理的に存在し得ない状態を捨てる手法他、古典コンピューターで効率良くシミュレーション可能な量子回路の結果と比較することによって結果を改善するクリフォードデータリグレッションと呼ばれる手法や、最もエラー割合の高い2量子ビットゲートのノイズを軽減するゼロノイズエクストラポレーションと呼ばれ手法などが知られている。 ↑


