永島 来悟（物理学専攻 大学院生）

辻 直人（物理学専攻 准教授）

Rafael Haenel（ブリティッシュコロンビア大学 大学院生）^*当時

Sida Tian（マックスプランク固体科学研究所 大学院生）

Dirk Manske（マックスプランク固体科学研究所 教授）

発表のポイント

• 超伝導秩序は光に反応しにくいと考えられていましたが、超伝導秩序が光に線形で応答する物質を判別する分類理論を構築しました。
• マルチバンド超伝導体において、熱力学的な自由エネルギーが「リフシッツ不変量」と呼ばれる対称操作によって変わらない不変量を持つと超伝導秩序が光に線形で応答することを見出しました。
• レーザー光を用いて超伝導秩序を高速に制御したり、あるいは光によってマルチバンド超伝導体の微視的性質を解明することへつながると期待されます。

マルチバンド超伝導体の光応答の概念図

---

発表概要

超伝導秩序を光によって制御したり増幅したりすることができないか、近年盛んに研究されています。超伝導秩序が強まると、より高い温度や強磁場の環境下でも超伝導状態を保つことができます。これまでは超伝導秩序と光の結合が弱く、特殊な状況を除いて超伝導秩序は光と非線形な応答しか示さないと考えられていました。ところが最近、マルチバンド超伝導体^（注1）に注目すると超伝導秩序が光に対して線形に応答する場合があるということが見つかってきています。しかし、一般に超伝導秩序が光に対して線形に応答するのはどのようなときか、また特に二次元や三次元の物質で現れるのはどのようなときかはわかっていませんでした。

東京大学大学院理学系研究科において永島来悟大学院生、辻直人准教授らは、ブリティッシュコロンビア大学のRafael Haenel大学院生(当時)、マックスプランク固体科学研究所のSida Tian大学院生、Dirk Manske教授らとの国際共同研究で、超伝導体の自由エネルギーにリフシッツ不変量^（注2）と呼ばれる対称操作で変化しない不変量が存在すると超伝導秩序が光に線形で応答することを見出し、それが現れるかどうかを判別する分類理論を構築しました。特に、超伝導秩序の集団励起モード^（注3）のうちバンド間の超伝導秩序の位相の差が振動するレゲットモード^（注4）を媒介して超伝導秩序が光に対して線形応答することがわかりました(図1)。これにより、レーザー光を用いて超伝導秩序を高速に制御したり、マルチバンド超伝導体の微視的性質を光によって明らかにすることにつながると期待されます。

図1：マルチバンド超伝導体のレゲットモードを媒介した光応答の概念図
マルチバンド超伝導体に光を照射すると、各バンドの自由エネルギー面上を球で示した秩序変数^（注5）が互い違いの方向に円周に沿って運動し、入射光の振幅に比例した振幅の光が放出される。このような秩序変数の運動はレゲットモードと呼ばれる集団励起モードに対応する。

発表内容

＜研究の背景＞
超伝導は物質の電気抵抗がゼロになり物質中の磁場を完全に排除するような「秩序立った状態」であり、その特性から多数の技術的応用が考案、実装されています。その微視的な性質をより一層理解するため、超伝導体に光を照射したときにどのような応答を示すかについて長年研究が行われてきました。特に近年レーザー光を中心とする技術の発展とともに、超伝導体の秩序を光によって高速に制御しようとする試みが多く行われてきています。従来、超伝導秩序と光の結合は弱く、特殊な状況を除いて光と非線形な応答しか示さないと考えられてきました。そのため、超伝導秩序を光によって変化させるためには高強度のレーザー光が必要でした。

超伝導体の秩序を特徴づける秩序変数は複素数であり、振幅と位相の自由度を持ちます。特にマルチバンド超伝導体では各バンドに対応して複数の秩序変数が存在します。例えば、マルチバンド超伝導体の一種としてカゴメ格子型の結晶構造を持つ超伝導体が挙げられます。カゴメ格子はその名の通り、日本の竹細工などで見られる編目模様(籠目)と似た形をしています。カゴメ格子超伝導体は最近発見された超伝導体で、カゴメ格子の構造に由来した特異な電子状態を持つことから注目されています。このようなマルチバンド超伝導体では、異なる秩序変数の位相の差が振動するレゲットモードと呼ばれる集団励起モードが新たに現れます。この振動モードは光に対して線形に応答する場合があることがわかってきていますが、一般にレゲットモードがどのような物質で光に対して線形に応答するのか、特に二次元以上の物質で可能なのかどうかはわかっていませんでした。

＜研究の内容＞
本研究では、マルチバンド超伝導体のレゲットモードが光に対して線形に応答するのは、熱力学な性質を記述する自由エネルギーにリフシッツ不変量と呼ばれる対称操作によって変わらない不変量が存在するときであることを見出しました。リフシッツ不変量は秩序変数について一階の空間微分を含む形をしており、物質が空間反転対称性を破るときにしか存在できないと考えられていましたが、本研究で、空間反転対称性の破れは必ずしも必要ではないことがわかりました。

超伝導体においてリフシッツ不変量が存在できるのはどのようなときかを、数学の一分野である群論を利用して全ての結晶構造とクーパー対の対称性について調べ上げました。群論は対称性を記述する数学の理論であり、着目する物質を不変に保つような対称操作に対してリフシッツ不変量が自明な表現を持つかどうかを確かめることによって、自由エネルギーにリフシッツ不変量が出現するかを判定できます。この結果をカゴメ格子超伝導体に適用したところ、通常のカゴメ格子ではリフシッツ不変量が存在しない一方、電子の飛び移りやすいボンドと飛び移りにくいボンドがあるようなカゴメ格子ではリフシッツ不変量が存在することがわかりました。実際に微視的な理論に基づいて線形応答領域の光学伝導度の計算を行うことで、後者の場合は超伝導ギャップ以下の周波数のところにレゲットモードに由来する共鳴ピークが現れることが確認できました(図2)。これ以外のパターンの不均一なボンドを持つカゴメ格子超伝導体についても分類理論を適用することで、光に線形で応答するレゲットモードが存在できるかどうかを調べることができます。

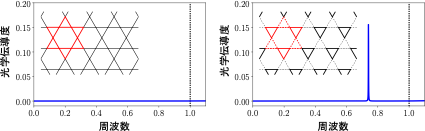図2：二つのカゴメ格子模型に対する光学伝導度スペクトルの比較
(左図)電子の飛び移りやすさが均一なカゴメ格子模型の光学伝導度の計算結果(青線)。リフシッツ不変量が存在しないことに対応し、レゲットモードの共鳴ピークが現れない。
(右図)電子の飛び移りやすいボンドと飛び移りにくいボンドを持ったカゴメ格子模型の光学伝導度の計算結果(青線)。リフシッツ不変量が存在することに対応し、超伝導ギャップ以下の周波数領域にレゲットモードの共鳴ピークが現れる。
縦の点線は超伝導ギャップの大きさに対応する周波数を示している。

＜今後の展望＞
リフシッツ不変量に由来して超伝導秩序が光に対して線形に応答することを利用すると、各バンドの超伝導秩序がどのような位相を持っているか、あるいはバンド間で超伝導秩序にどのような微視的相互作用が働いているかがわかると期待されます。これはカゴメ格子超伝導体などのマルチバンド超伝導体の微視的な性質を解明することにつながります。また、レーザー光を用いて超伝導秩序を高速に制御し、あるいは光によって超伝導秩序を誘起・増幅することへの足掛かりになると考えられます。

論文情報

雑誌名	Physical Review Research
論文タイトル	Classification of Lifshitz invariant in multiband superconductors: an application to Leggett modes in the linear response regime in Kagome lattice model
著者	Raigo Nagashima＊, Sida Tian, Rafael Haenel, Naoto Tsuji, and Dirk Manske
DOI番号	10.1103/PhysRevResearch.6.013120