DATE2023.12.14 #Press Releases
スピンを薄めることで巨大な磁場応答を実現
――反強磁性スピントロニクスへの応用に期待――
諏訪 秀麿(物理学専攻 助教)
発表のポイント
- 反強磁性スピンの密度を下げることで巨大な磁場応答を得ることに成功しました。
- 希釈によるスピン異方性の制御を理論的に解明し実験的に実証しました。
- 反強磁性体を用いたスピントロニクスにおける効率的な操作への応用が期待されます。
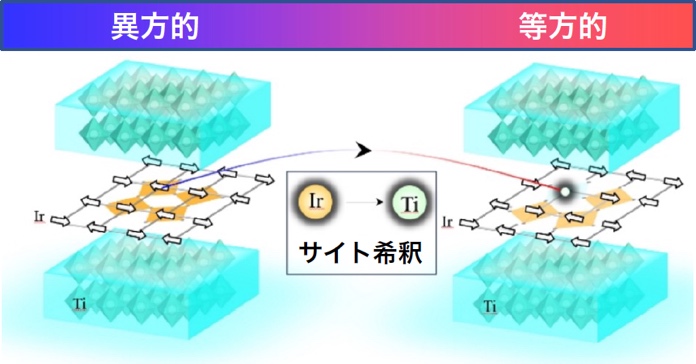 スピンの希釈による異方性制御
スピンの希釈による異方性制御
発表概要
東京大学大学院理学系研究科の諏訪助教は、テネシー大学、中国科学院、アルゴンヌ国立研究所、ブルックヘブン国立研究所、オクラホマ州立大学、カレル大学、ダブリンシティ大学の研究グループと共同で、反強磁性スピンを希釈してスピン異方性を制御し、巨大な磁場応答を得るメカニズムを理論・実験の両面から実証しました(図1)。本研究では超格子(注1)中における元素比の制御技術を用いることで、反強磁性体であるイリジウム酸化物のイリジウムをチタンに置き換えるサイト希釈を施しました。その結果、サイト希釈率50%において、スピン相互作用のわずか0.1%のエネルギーに相当する0.5テスラの磁場で磁気転移温度を600%も上昇させる巨大な磁場応答を世界で初めて観測しました。先行研究と比較して、サイト希釈を用いたスピン異方性の制御を通じて巨大な磁場応答を実現した点で新規性があり、この研究成果は今後反強磁性スピントロニクスにおける効率的な操作に役立つことが期待されます。
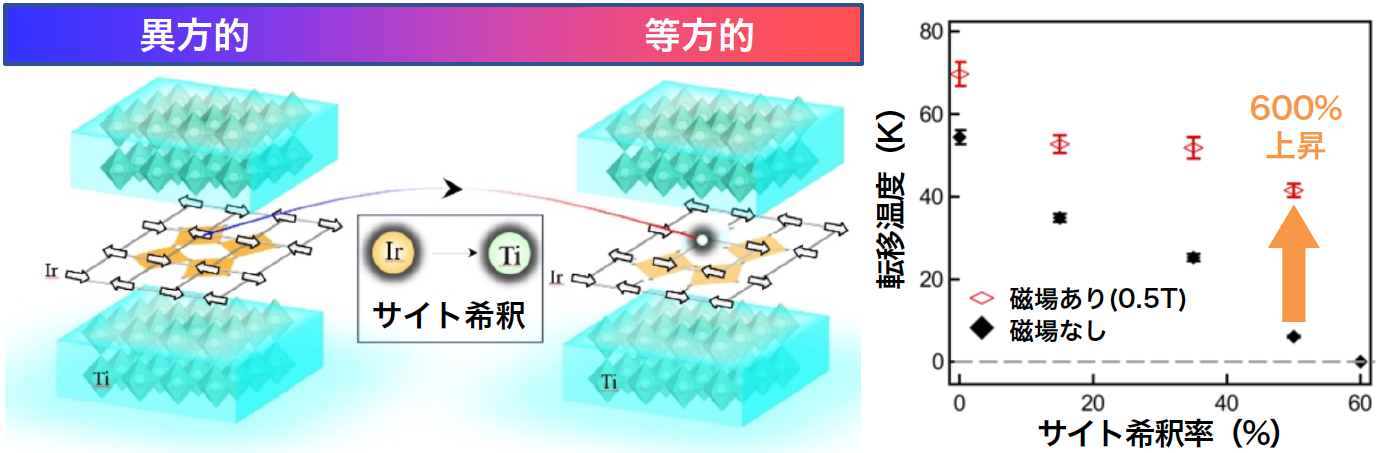 図1:サイト希釈によるスピン異方性の制御と磁場による転移温度の上昇
図1:サイト希釈によるスピン異方性の制御と磁場による転移温度の上昇
(左図)イリジウム(Ir)をチタン(Ti)に置き換えるサイト希釈によってスピン異方性が実効的に消失します。
(右図)磁場なしと磁場0.5テスラ(T)での磁気転移温度のサイト希釈率依存性。Nano Letters, 2023, DOI: 10.1021/acs.nanolett.3c02470 より改変。
発表内容
電子の持つスピンを操作することで不揮発性、低消費電力といった理想的な機能を実現するスピントロニクスの研究が盛んに行われています。中でも反強磁性スピンを効率的に操作することができれば、高速かつ大容量なデバイス開発につながると大きく期待されています。しかし反強磁性スピンは互いに反対向きにそろう性質があるため正味の磁化が打ち消し合い、一般的に磁場応答が小さくスピンの操作は難しくなります。先行研究では、スピン軌道結合(注2)から生じる反強磁性スピンのわずかな傾きを利用した磁場操作が行われていました。しかし通常、スピンを傾かせるためにスピンの異方性が生じてしまい、その結果磁場応答が小さくなってしまうことが問題となっていました。
もし2次元系の反強磁性スピンで傾いた磁気秩序を取りつつもスピン等方的な物理系が実現できれば、巨大な磁場応答を得ることが可能となります。この度、本研究チームはそのような不可能とも思える物理系の実現に着想を得て、世界で初めてサイト希釈を用いたスピン異方性の制御と巨大磁場応答を理論・実験の両面から実証しました。研究チームは、2次元系のスピン異方的な反強磁性体において希釈率が閾値を超えると、実効的にスピン等方的な強い磁場応答を得られることを理論的に示しました。その理論に基づき、強い2次元性を持つ超格子 [(SrIrO3)1/(SrTiO3)2]を基礎として、スピンを持つイリジウム(Ir)を、スピンを持たないチタン(Ti)に置換することで、さまざまなサイト希釈率の薄膜を合成しました。この物質は低温でわずかに傾いた反強磁性秩序を示します。共鳴X線磁気散乱(注3)を用いて反強磁性秩序パラメータの磁場温度依存性を測定し、希釈率50%の場合、スピン相互作用(50 ミリ電子ボルト)のわずか0.1%のエネルギーに相当する磁場(0.5テスラ)で反強磁性転移温度を600%も上昇させる巨大な磁場応答を観測しました(図2)。希釈率0%、15%、35%の場合は異方的モデルで説明できるのに対し、希釈率50%の場合は等方的モデルを用いた理論計算とよく一致し、転移温度の大幅な上昇に成功しました。東京大学のグループが中心となり希釈によるスピン等方的な磁場応答のメカニズムを理論的に解明し、量子モンテカルロ法(注4)による計算と組み合わせることで、実験的に観測された転移温度の上昇を定量的に説明しました。今回明らかにした希釈による異方性の消失はさまざまな物質に応用でき、将来的な反強磁性スピントロニクスにおける効率的スピン操作につながると期待されます。
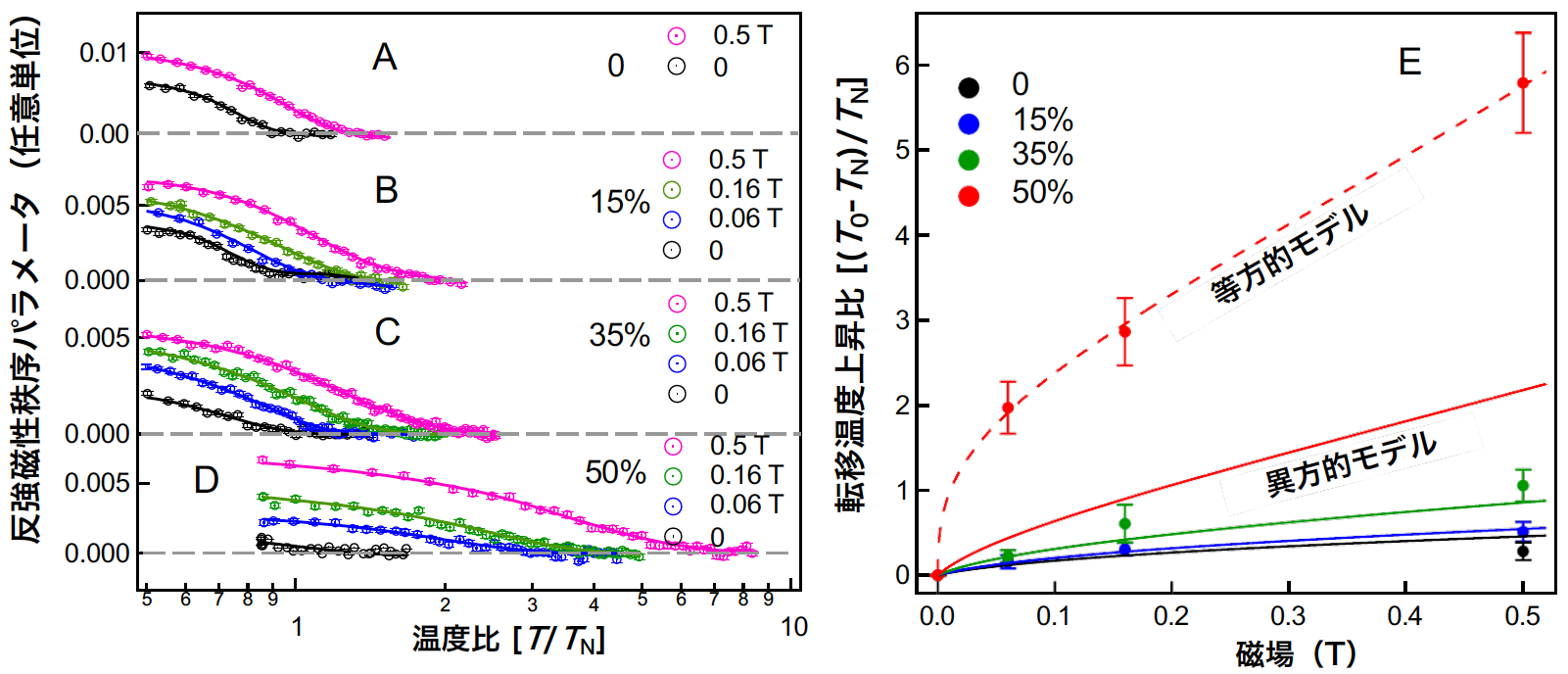 図2:反強磁性秩序の温度依存性と転移温度の磁場依存性
図2:反強磁性秩序の温度依存性と転移温度の磁場依存性
(左図)共鳴X線磁気散乱から得られた反強磁性秩序パラメータの磁場温度依存性。サイト希釈率は(A)0%、(B)15%、(C)35%、(D)50%。横軸は磁場なしでの転移温度(TN )との比で、磁場は0、0.06、0.16、0.5テスラ(T)を印加。(右図)転移(クロスオーバー)温度(T0)の上昇比の磁場依存性。希釈率0%、15%、35%の場合はスピン異方的なモデルを用いた理論計算(実線)で説明できるのに対し、希釈率50%の場合はスピン等方的なモデルを用いた理論計算(破線)とよく一致し、転移温度が大幅に上昇します。Nano Letters, 2023, DOI: 10.1021/acs.nanolett.3c02470 より改変。
論文情報
-
雑誌名 Nano Letters 論文タイトル Extraordinary magnetic response of an anisotropic 2D antiferromagnet via site-dilution 著者 Junyi Yang, Hidemaro Suwa*, Derek Meyers, Han Zhang, Lukas Horak, Zhan Zhang, Evguenia Karapetrova, Jong-Woo Kim, Philip J. Ryan, Mark P. M. Dean, Lin Hao*, and Jian Liu* DOI番号 10.1021/acs.nanolett.3c02470
用語解説
注1 超格子
複数の種類の結晶格子が組み合わさり、各結晶だけの場合より長い周期の構造を持つ結晶格子。↑
注2 スピン軌道結合
相対論的効果から生じる、電子のスピンと軌道角運動量の間の相互作用。↑
注3 共鳴X線磁気散乱
内殻電子と外殻電子のエネルギー差に対応するX線による回折を用いて、強い散乱強度を得る実験手法を共鳴X線散乱といいます。直線偏光したX線を用いることで、電荷による散乱と磁気モーメントによる散乱を分けることができ、このようにしてスピン秩序を調べる手法を共鳴X線磁気散乱と呼びます。↑
注4 量子モンテカルロ法
確率的なサンプリングによる平均値として物理量を計算する方法をモンテカルロ法と呼びます。この手法をスピン系などの量子力学に従う物理系に応用した計算法が量子モンテカルロ法です。↑


