DATE2021.10.12 #プレスリリース
化学反応において普遍的に成り立つ非平衡熱力学法則を導出
吉村 耕平(物理学専攻 修士課程2年生)
伊藤 創祐(生物普遍性研究機構/物理学専攻 講師)
発表のポイント
- 化学反応において普遍的に成り立つ、2つの熱力学なトレードオフ関係(注1) を発見。
- 確率的に振る舞う系でしか知られていなかった法則が決定論的(注2)に変化する化学反応系でもなりたつことを、一般的な仮定のもとで示した。
- 熱力学的なトレードオフ関係の普遍性を示すと共に、生体内の代謝系や情報伝達系をはじめとする自然界の化学反応の熱力学的解析に新たな指針を与える。
発表概要
ブラウン運動や分子モーターのような確率的に振る舞う非平衡系(注3)の熱力学的性質に関する研究が、近年盛んに行われています。ゆらぎの熱力学と呼ばれるその枠組みにおいて、これまでにさまざまな熱力学法則が発見されてきました。
一方、非平衡系は確率的に振る舞うものだけではありません。たとえば、決定論的な化学反応は生体内をはじめ身近に見られる重要な非平衡現象です。しかし、ゆらぎの熱力学の発展とは対照的に、非平衡状態にある化学反応系がどのような熱力学的性質を持つかはあまり知られていませんでした。
東京大学大学院理学系研究科の吉村耕平大学院生と伊藤創祐講師は、従来注目されていなかった化学反応が内在的に持つゆらぎの指標を利用することで、決定論的な化学反応においても、ゆらぎの熱力学で得られてきた熱力学的トレードオフ関係である熱力学的不確定性関係と熱力学的速度限界が得られることを発見しました。
本研究はこれらの非平衡熱力学法則が本質的に異なる系で成り立つことが明らかにし、法則の普遍性を支持するものとなりました。また今回証明された関係を用いることで、これまで個別かつ具体的な化学反応系で行われてきた熱力学的解析が統一的な視点から行われ、化学反応を用いた生体内のプロセスへの理解が深められることが期待されます。
本研究成果はPhysical Review Letters誌に10月11日付(現地時間)で掲載されます。また、Editors’ Suggestionに選ばれました。
発表内容
世の中の現象の大半は非平衡現象です。そのため、平衡状態を記述する熱力学・統計力学の枠組みが20世紀初頭に完成して以降、非平衡系の持つ性質が長らく研究されてきました。ゆらぎの熱力学と呼ばれる分野の進展によって、ブラウン運動や分子モーターのような確率的に振る舞う非平衡系の持つ熱力学的性質が、この20年で徐々に明らかにされてきました。
一方、非平衡系は確率的に振る舞うものだけではありません。その代表例が決定論的な化学反応です。正味の反応が進行中である化学平衡にない化学反応系や、生き物の体内のように外部と物質のやりとりがある化学反応系が、非平衡な化学反応系の例です。これらの現象は、系のサイズが十分大きい場合決定論的に振る舞うため、ゆらぎの熱力学の理論を用いることはできません。決定論的な化学反応の熱力学理論は化学熱力学と呼ばれる分野において古くから研究されてきましたが、平衡熱力学の範疇を大きくは超えないものでした。最近ではゆらぎの熱力学の成功に喚起され少しずつ非平衡理論の研究も行われるようになってはきたものの、未だそれほど盛んとは言えません。特にゆらぎの熱力学で発見された非平衡系の諸性質が、化学熱力学でも成り立つかはほとんど知られていませんでした。
東京大学大学院理学系研究科の吉村耕平大学院生と伊藤創祐講師は、ゆらぎの熱力学で得られた非平衡熱力学法則の中でも特に昨今注目を集めている熱力学的不確定性関係(TUR : Thermodynamic Uncertainty Relation)と熱力学的速度限界(TSL : Thermodynamic Speed Limit)という二つの法則が、化学熱力学の枠組みでも成立することを証明しました。以下、TURおよびTSLについてそれぞれ説明していきます。
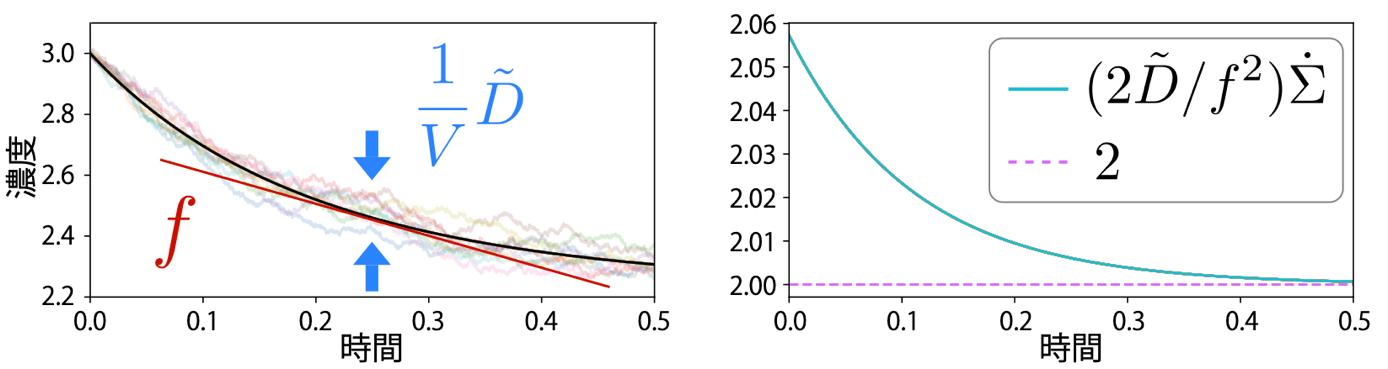
図:スケールされた拡散係数と、化学反応における熱力学不確定性関係の概念図。
(左)濃度の時間変化は系が大きくなることで確率的な振る舞い(薄い線)から決定論的な振る舞い(黒線)に収束する。このとき小さくなっていくゆらぎの大きさは体積の逆数1/Vに比例し、そこからスケールされた拡散係数が得られる。スケールされた拡散係数はこのように確率的なゆらぎと関係を持つものの、決定論的なダイナミクスにおける物理量のみを用いて定義可能である。
(右)単位時間あたりの散逸(エントロピー生成率)∑と、濃度変化の速度 ƒ に対するスケールされた拡散係数Dの大きさD/ƒ 2で表されるゆらぎとの積はある一定の値(図中点線)を下回ることができない。すなわち、これらの量を同時に好きなだけ小さくすることはできない。図中では歴史的な経緯から2がかけられている。
次に、TSLの説明の前に一般の速度限界について説明します。速度限界とは系が変化する際必要な時間に対する下限です。逆に言うと、ある状態から別の状態に変化させる際かかる時間は速度限界が存在するとき、その速度限界より短くすることができません。ここ数年、量子・古典を問わず種々の物理系において様々な速度限界が存在することが示され、注目を集めてきました。特に非平衡過程における散逸を用いた速度限界を、熱力学的速度限界(TSL)と呼びます。TSLは一般的に、散逸を小さくするとその分長い時間がかかる(正確には、かかる時間を短くできなくなる)ことを表現します。ゆらぎの熱力学において発見されたTSLでしたが、散逸自体はゆらぎと直接の関係がないため決定論的なダイナミクスでも得られるはずでした.本研究では、再びスケールされた拡散係数を用いることで、決定論的な化学反応においてもTSLが得られることを証明しました。
これらの結果の一般性も本研究の特徴の一つです。これまで化学反応にまつわる結果は、分子間の相互作用を無視する系の理想性を仮定したものが多く、一般性には不満の残るものがほとんどでした。詳細は省きますが、本研究の結果は一般化された局所詳細釣り合い関係と呼ばれる物理的仮定を用いることで、非理想な系を含む一般的な状況下で成り立つものとなりました。また決定論的化学反応では化学振動のような非線形現象(注4)が生じますが、そのような場合も本研究の結果は成立します。論文内ではロトカ–ヴォルテラ方程式を用いた数値実験によって、化学振動を示す場合にもトレードオフ関係が成り立つことを確認し、同時に不等式の性能評価も行いました。その結果、化学振動を示す系でも有用な不等式関係になっていることが確認されました。
本研究はこれまで確率的に振る舞う系でしか証明されてこなかった非平衡熱力学法則 (TUR およびTSL)が、決定論的な化学反応という本質的に異なる系でも成り立つことを示し、法則が幅広い現象で成り立つこと、すなわちその普遍性を証明しました。
またその意義は観念的なものに留まりません。生体内では代謝や情報伝達・情報処理など、さまざまなプロセスに化学反応が利用されています。その収率や正確さと、コストの間のトレードオフ関係は古くから盛んに研究されてきましたが、それらの研究は個別具体的ないし特殊な化学反応系において得られた結果でした。そのため一般的な枠組みに基づく本研究の結果が、生体内の化学反応を統一的に考察する視点を新たに与え、包括的な理解を深める助けとなることが期待されます。
本研究は科学研究費補助金新学術領域(研究領域提案型)「情報物理学でひもとく生命の秩序と設計原理」 の計画研究班「情報熱力学による生体情報処理の理論研究」科研費番号(19H05796)および戦略的創造研究推進事業さきがけ「情報幾何と熱力学による生体コンピューティング理論」(JPMJPR18M2)、UTEC-UTokyo FSI Research Grant Programの支援を受けて行われました。
発表雑誌
-
雑誌名 Physical Review Letters 論文タイトル Thermodynamic uncertainty relation and thermodynamic speed limit in deterministic chemical reaction networks著者 Kohei Yoshimura*, Sosuke ItoDOI番号 10.1103/PhysRevLett.127.160601 論文URL https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.127.160601
用語解説
注1 トレードオフ関係
2つの量を同時に効率化できない関係のこと。日常語として使われることもあるが、非平衡熱力学では特に関心を集めるテーマでもある。本研究で証明された熱力学的不確定性関係はゆらぎと散逸のトレードオフ関係であり、熱力学的速度限界は速度と散逸のトレードオフ関係であると言える。化学反応においては、例えば細胞内におけるエネルギーの通貨として知られる生体分子であるATPの生成における生成の効率(収率)と速度の間のトレードオフ関係(T. Pfeiffer, et al., Science 2001)など実験・理論によって種々のトレードオフ関係が知られていたが、それらはいずれも化学反応の種類を限定したものであった。↑
注2 決定論と確率論
系の時間変化において、初期条件を同じにすればその後の物理量の変化が1通りのものを決定論的、ランダム性があり1通りでないものを確率的ないし確率論的という。少ない分子数で実験を行えば化学反応は確率的に起こり濃度の変化は試行毎に異なるが、分子数が多ければ濃度の変化は決定論的に進み、毎回一定のものになる。化学反応の1回の起こる/起こらないはランダムでも、分子の数が十分多ければ(たとえばアボガドロ数 6✖️1023 個程度あれば)、濃度の変化にランダム性は現れなくなる.生体内の化学反応では関与する分子数が多いものも少ないものも存在するが、両方なくてはならない存在である。↑
注3 非平衡系/現象
十分長い時間放置し、変化がなくなるまで待つことで得られる状態を平衡状態と呼ぶのに対し、時間の経過とともに変化している状態や一見変化がないものの外部と熱や物質のやりとりがある状態を非平衡状態と呼び、非平衡状態にある系(物理的対象)を非平衡系、非平衡状態における現象を非平衡現象と呼ぶ。例えば、ビーカーの中に薬品を入れて蓋をしておけば、系はいずれ平衡状態に到達する。一方、平衡に至る前で正味の化学反応が進行中であったり、外部から物質の供給と回収が行われていたりする場合、系は非平衡状態にある非平衡系である。熱力学は平衡系の有する普遍的な性質を記述するが、非平衡系・非平衡現象におけるそのような理論の構築の試みが古くから行われている。↑
注4 化学振動、非線形現象
非線形現象とは相互作用の非線形性から引き起こされる現象のことで、カオスや乱流、化学振動などを含む。化学振動とは、化学反応が進む際に濃度が周期的に変化する現象で、最初に発見されたベロウソフ–ジャボチンスキー反応(BZ反応)が最も有名な例である。BZ反応では、溶液の色が数秒ごとに変化することから演示実験などによく用いられ、動画サイトで「BZ反応」などと調べると多くの動画を確認することができる。化学振動を示すモデルは多く存在するが、本研究ではロトカ–ヴォルテラ方程式(元々捕食者と被食者の個体数変化を表し、時間的に振動する解を持つ微分方程式)を化学反応のモデルとして利用し、結果の確認を行なった。↑


