Disclaimer: machine translated by DeepL which may contain errors.
~ A message from a graduate student
Symmetry of Invisible Forms
 |
| Kan Kitamura |
| Graduate School of Mathematical Sciences, 1st Year Research Student |
| Place of birth Kyoto Prefecture |
| High School Nada Private High School |
| Faculty Department of Mathematics, Faculty of Science, The University of Tokyo |
There are various symmetries around us. For example, the earth has rotational symmetry about the earth's axis if we consider it as a sphere. We humans have roughly symmetrical body parts such as limbs. Crystals such as salt also have various symmetries depending on the type of molecule. A doughnut has rotational symmetry about an appropriate axis passing through the center of the hole if there is no surface irregularity.
Next, let us look at a doughnut with an uneven cross-section and a twisted dough. As shown on the left side of the figure, the dough is extruded into a Y-shape and twisted at a constant speed for exactly one revolution to form a loop. Here, the Y-shaped cross section is assumed to have 120° rotation symmetry. One of the edges is covered with chocolate. If we rotate it by 120° as shown in the left side of the figure, the shape is the same as the original, but the arrangement of the chocolate is different. In order to adjust this arrangement, the doughnut must be twisted inward (right side of the figure). In other words, this chocolate doughnut is in a situation of 120° rotational symmetry with some correction.
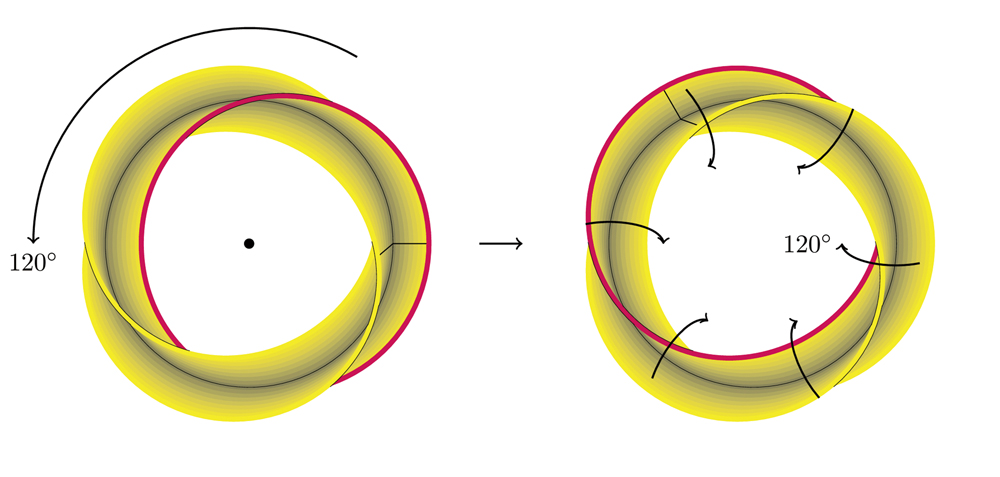
Schematic of the twisted doughnut. Chocolate is shown in red. The right side shows the donut after 120° rotation in the direction shown on the left, and the inward twisting operation to adjust the color to the left.
Such "twisted" symmetries also appear in my field of mathematics, noncommutative geometry. In noncommutative geometry, we consider a special collection of matrices (which may have an infinite number of components). A collection of matrices sounds algebraic, but in fact it gives the notion of an extension of space. It is not a space in the usual sense, however, and we cannot see its "form" in person, but it can still be given a geometric meaning. On the other hand, unlike ordinary numbers (integers, real numbers, etc.), matrix multiplication often changes its answer when the order is exchanged. Because of this situation, forms in noncommutative geometry exhibit strange properties that go beyond our intuition. This new phenomenon attracted me to this field.
The concepts called quantum groups and tensor spheres appear as symmetries of such noncommutative geometries. In a sense, the chocolate doughnut example introduced above can be regarded as having such symmetries behind it. These symmetries are also difficult to see directly, but they are closely related to a theory of physics called quantum field theory, which describes the behavior of particles and other objects, and is the source of a rich theory. In order to deepen our understanding of these new symmetries, I am working on new ways of constructing the symmetric forms of quantum groups and tensor spheres, and on tools for extracting their properties.
It is often said that mathematics is a useless subject. I myself do not believe that my research is actually useful to the world. On the other hand, however, mathematics plays a role as a kind of soil that gives words to describe other sciences. And I believe that what enriches this soil is the interest and depth of mathematics itself as a science. As I mentioned in the title "Invisible Forms," noncommutative geometry is described in the formal language of mathematics. However, even though it is formal, it is not dry, and it contains free ideas to deal with new phenomena. And there are mysterious landscapes that can be felt only by unraveling them.
Finally, I hope that this article will help readers to pursue a career in science.


