Disclaimer: machine translated by DeepL which may contain errors.

Statistical Laws and Population Adaptation Explored by Back-to-Back Comparison of Bacteria

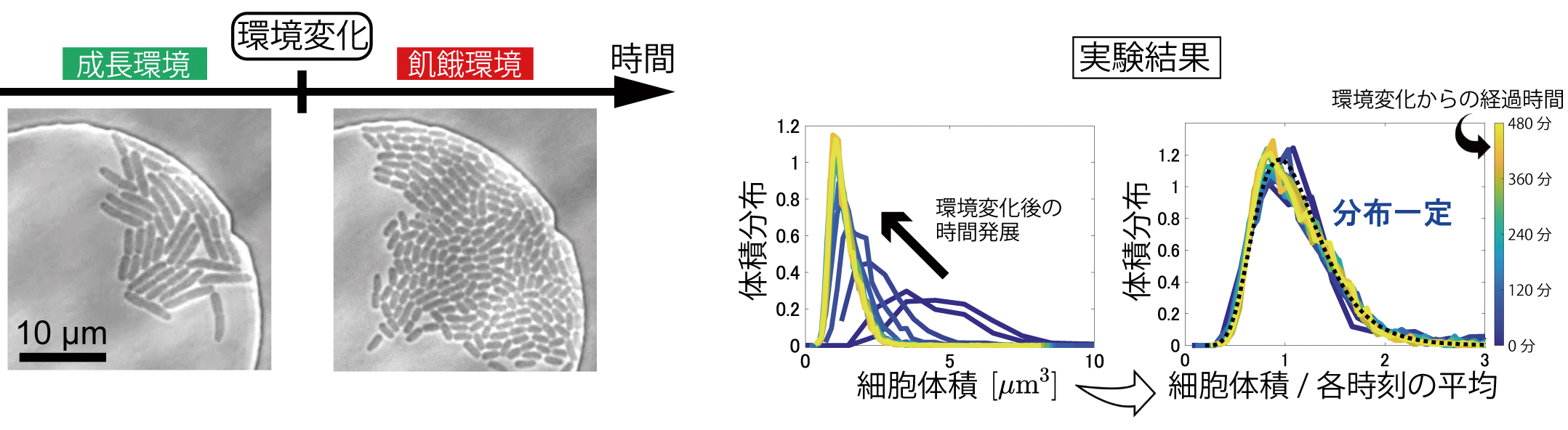
Some of us are tall and some of us are not, but we rarely pay attention to them. Microorganisms composed of single cells also have large and small individuals, and if they were intelligent, the same would be true. However, in an environment rich in nutrients and favorable to the cell, the cell grows and enlarges, then divides, reducing its size by half. In other words, since cell size is determined by a combination of growth and division, if we can find rules underlying growth and division by measuring cell size, we can obtain clues to the cellular mechanism. For example, in bacteria such as Escherichia coli, it has been observed under various conditions that after division, the next division occurs after a certain amount of increase in length, and research on the relationship between gene replication and the cell cycle is ongoing. In single-celled eukaryotes, it has been reported that the distribution of cell size is represented by a common functional form, even in different species. However, these previous studies have only focused on the constant regularity and distribution law observed in a stationary environment with constant nutrient concentration and temperature, and there is little quantitative information on the nature of cell size under more natural, fluctuating conditions.

We were interested in the cell size distribution of bacteria in fluctuating environments, and developed a device that can uniformly and controllably change the culture environment for a large number of individual bacteria and made measurements. After allowing a population of E. coli to grow, divide, and multiply vigorously in a nutrient-rich, steady-state environment, the bacteria were suddenly switched to a nutrient-free environment and starved. The growth of the bacteria slows down, but they continue to divide to some extent, resulting in a decrease in volume. We performed a statistical analysis of this time-varying cell volume distribution and found that the bacterial population satisfies a statistical property called "scale invariance," in which the mean volume shrinks but the distribution of the volume ratio to the mean remains unchanged. This property was reproduced in the simulation of a bacterial cell cycle model that had been proposed based on studies in a steady-state environment, and is expected to be widely applicable to bacterial populations. In the simulation, we also found that slow starvation induces a transition phenomenon that breaks scale invariance.

	Figure: Left: E. coli before and after starvation. Right: Scale invariance of cell volume distribution. With starvation, the volume shrinks, but the distribution of the ratio of volume to mean remains constant. Source: T. Shimaya et al., Commun. Phys. 4, 238 (2021). https://doi.org/10.1038/s42005-021-00739-5

What does it mean for a bacterial population that the volume distribution exhibits scale invariance?　We do not yet have the answer, but it is becoming clear that many life phenomena in bacterial populations are caused by mechanical factors such as movement and pushing and shoving. The finding that the distribution of volume ratios does not change with environmental changes implies a certain robustness in these mechanical population characteristics, and we have begun to consider whether this may be a new aspect of collective adaptation exhibited by bacteria.

The results of this study were published in T. Shimaya et al, Commun. Phys. 4, 238 (2021).

(Press release November 10, 2021)

Published in Faculty of Science News, March 2022

Communicating to Faculty Research Students >