Disclaimer: machine translated by DeepL which may contain errors.
What are the Rules of Slow Earthquakes?
Satoshi Ide, Professor, Department of Earth and Planetary Science
Various slow earthquakes are quietly occurring underground.
The scale rule that defines the time and magnitude of these phenomena has been verified for the first time in 16 years using the latest data.
The hypothesis that slow earthquakes are a universal phenomenon that proceeds according to this law is now closer to being established.
We may need to rethink the idea that slow earthquakes are a phenomenon that occurs anywhere and anytime in the Earth's interior, and that ordinary earthquakes are rather anomalous deformations of the Earth's interior.
When strong forces are applied to the rock in the Earth's interior, faults in the rock rupture and slide rapidly, causing earthquakes. The powerful seismic waves of a major earthquake can trigger an earthquake disaster. However, there is a phenomenon in which the rock mass is ruptured and slides slowly, and thus almost no seismic waves are emitted, even though this phenomenon is the same as an earthquake. This is the slow earthquake discovered in this century.
What is the difference between a slow earthquake and an ordinary earthquake? This research clarified this question as a difference in the scale law that expresses the difference in the magnitude of the phenomenon from a physical point of view.
First, there is a well-known scale law for normal earthquakes. Small earthquakes end quickly, while large earthquakes last for a long time. Let T be the duration of the destruction of the bedrock, and T increases tenfold for every two increases in the magnitude of the earthquake. This relationship can be expressed as M0 is proportional to the cube of T, using the seismic moment Note M0, which is currently used as a unit of seismic magnitude.
Slow earthquakes are also large and small, and their seismic moment M0 also increases with duration T. However, M0 appears to be proportional to the first power of T. In 2007, a hypothesis was proposed that slow earthquakes, both large and small, are universal phenomena governed by a scale law different from that of ordinary earthquakes. Because of its importance, this hypothesis has generated much debate among seismologists over the past 16 years.
Initially, the hypothesis was subjected to some criticism because of the scattered and poor data. However, over the past 16 years, numerous studies have accumulated data with good continuity, ranging from less than 1 second to nearly 1 year for T, or about 8 orders of magnitude. This data supports the hypothesis that M0 is proportional to T. On the other hand, this study shows that most of the criticisms against the hypothesis are due to improper data processing. However, it was also revealed that small slow earthquakes were not detected due to observation limits, and the proportionality between M0 andT was reinterpreted as a law that defines the limit of the magnitude M0 of a slow earthquake lasting only for time T, rather than a one-to-one relationship.
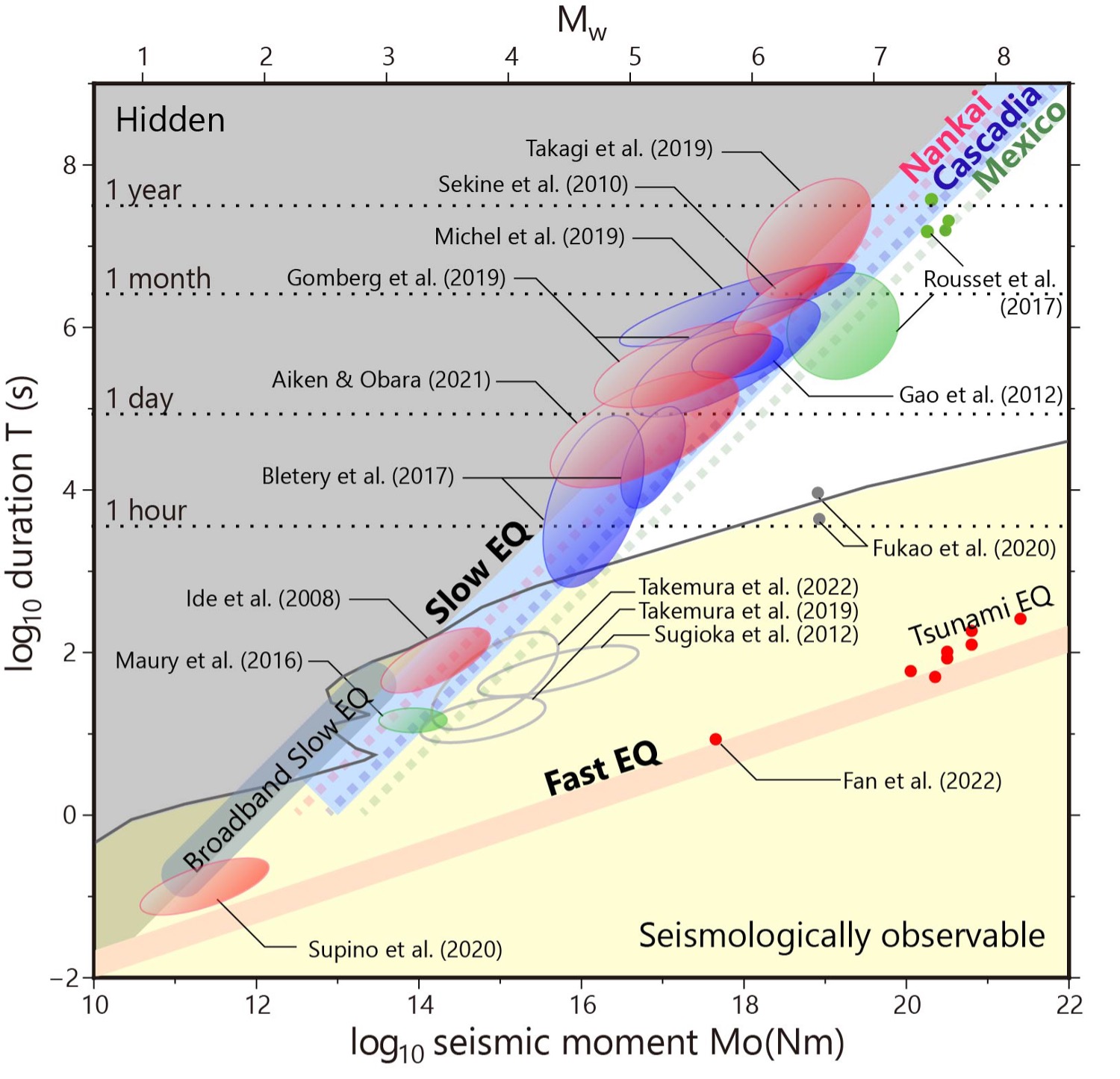Scale law for slow earthquakes (relationship between M0 andT ) and fast earthquakes
Slow earthquakes of various sizes are now observed in many parts of the world, and their existence has become commonplace. It is suggested that slow earthquakes are more universal than earthquakes as a destructive slip phenomenon in the earth's interior. The scale law, which indicates the limit of the universal phenomenon, seems to tell us that "ordinary earthquakes," which do not follow the limit of the universal phenomenon, are anomalous phenomena. How does a universal phenomenon (slow earthquake) switch to an anomalous phenomenon (earthquake)? Research on the relationship between the two has just begun.
The results of this study were published in S. Ide et al., Proc. Natl. Acad. Sci. U. S. A. (PNAS), 120, (32)e2222102120, 2023.
Note: Seismic moment
The magnitude of rotational motion (in Nm) caused by the motion of a fault during an earthquake. It is equal to the amount of slip of an earthquake fault integrated over the fault plane and multiplied by the rigidity of the rock mass. The seismic moment can be converted to magnitude on a one-to-one basis. For every two magnitudes increase in magnitude, the seismic moment increases by a factor of 1000.
(Press release, August 1, 2023)
The Rigaku-bu News, November 2023
Frontiers of Science for Undergraduates