Disclaimer: machine translated by DeepL which may contain errors.

Nested Structures Fight Noise in Quantum Computers

Hayata Yamazaki, Assistant Professor, Department of Physics

Human beings now have the technology to control microscopic physical phenomena occurring in atoms and weak light with high precision according to the laws of quantum mechanics.
Quantum computers are attracting attention as a potential application of such quantum technology.
Conventional computers perform calculations using bits, which are 0s and 1s, as the unit of information processing.
Quantum computers use qubits in a superposition of 0s and 1s, enabling advanced information processing that is difficult to achieve with conventional computers.
In our research, we have developed a method that greatly improves the efficiency of the procedure for executing calculations on a quantum computer, and have made great strides toward its realization.

A quantum computer consists of many qubits, but the quantum information carried by the qubits is fragile, and errors inevitably occur due to the influence of small noise during the computation. Therefore, in order to realize a large-scale quantum computer, it is essential to have a mechanism for "error-resistant quantum computation," in which the computation proceeds while protecting the information from errors. Error-tolerant quantum computation uses a code that represents the information in a qubit by a larger number of qubits to correct errors that occur in individual qubits while proceeding with the computation. Currently, actual quantum computers, which are being developed worldwide, are unable to perform error correction sufficiently, so they cannot correctly perform large-scale calculations due to the effects of noise that accumulates. However, if error-resistant quantum computation becomes possible through future technological development, it is expected to lead to the realization of useful quantum computers that can perform large-scale calculations.

However, error-resistant quantum computation requires the addition of many qubits and a complicated calculation procedure, so it is difficult to design a calculation procedure that strikes a good balance between a small number of qubits (high efficiency) and high calculation speed (high speed). Existing theoretical research methods on error-resistant quantum computation have led to a situation in which either high efficiency or high speed is sacrificed to a large extent. For example, the method proposed in the early research on error-resistant quantum computation increased the error correction capability by nesting simple codes that protect a single qubit of information from noise. Because of the simplicity of the nested structure, the computation can be performed relatively fast. However, it required a large number of qubits, making it inefficient.

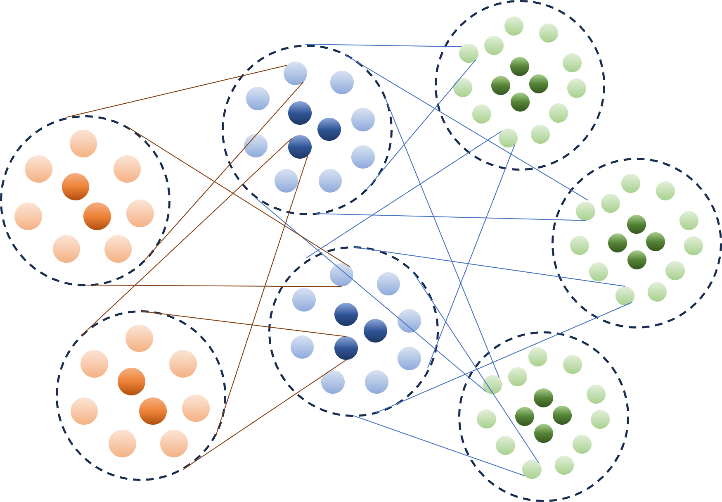Nested structure of qubits to create error tolerance

In response to this problem, this research has developed a new error-resistant method that uses not one but multiple simple codes that protect multiple qubits as a code with a special nested structure (Figure). The nested structure of combining simple codes reduces the computation speed, and at the same time, by using codes that protect multiple qubits, the number of qubits is reduced and efficiency is improved. This overcomes the shortcomings of the conventional nested structure and enables both high efficiency and high speed for the first time. In conventional nested codes, it is necessary to increase the number of additional qubits by 10, 100, or 1,000 to protect the information of a single qubit, thereby increasing the error correction capability. In the proposed method, however, the error correction capability can in principle be increased as much as possible by adding only about 40 qubits per qubit. Therefore, the proposed method opens up the possibility of reducing the burden of hardware development for the realization of large-scale quantum computers, and is expected to be widely used as a fundamental technology in the development of quantum computers in the future.

This research result was published in H. Yamasaki and M. Koashi, Nature Physics 20, 247 (2024).

(Press release on January 16, 2024)

Published in The Rigakubu News May 2024

Frontiers of Science for Undergraduates >