Erik Lötstedt, Associate Professor, Department of Chemistry

Kaoru Yamauchi, Professor, Department of Chemistry

Yutaka Tachikawa, Director, Data Science Center, QCC Project, DIC Corporation

 

Key points of the presentation

• Vibrational energy levels of the _{CO2 molecule} were calculated using the quantum computer ibm_kawasaki.
• By applying the newly developed hybrid eigenvalue algorithm ^{(Note 1) and} a simple error suppression method, the Fermi resonant vibrational state of _CO2 was calculated with high accuracy.
• The results show that the quantum computer is promising for the calculation of vibrational energy levels of polyatomic molecules and that the quantum computer is useful for spectroscopic studies of molecular vibrations.

 

Summary of Presentations

One promising area of application for the quantum computer ^{(Note 2)} is the calculation of quantum mechanical energy levels of atoms and molecules. However, when calculations are performed using current quantum computers, the results contain errors due to various sources of noise. Therefore, an important issue in quantum computing research is the development of methods to reduce the effects of noise.

In the "Applied Quantum Chemistry with Qubit (AQUABIT)" project ( https://www.u-tokyo.ac.jp/adm/fsi/ja/projects/quantum/project_00064.htmlを参照 ), a research group led by Associate Professor Eric Rotstedt and Professor Kaoru Yamauchi Professor Yamauchi's research group is developing new methods and algorithms for simulating atomic and molecular systems on a quantum computer in collaboration with Yutaka Tachikawa's team at DIC Corporation. In this study, Roetzstedt, Yamauchi, and Tachikawa demonstrated that the energy ^{(Note 3)} of the vibrational level of the _{CO2 molecule} can be accurately calculated on a quantum computer.

In this study, they developed a new hybrid method for calculating vibrational energy levels using both a quantum computer and a classical computer ^{(Note 4)}. The calculations on the quantum computer were performed using ibm_kawasaki^{(Note 5),} a superconducting quantum computer manufactured by IBM, which was installed in Shin-Kawasaki last year. By comparing the energies obtained on the quantum computer with reference results obtained on a classical computer, a simple error suppression method was introduced to estimate systematic errors due to noise, and the level energy of the Fermi resonance level ^{(Note 6)} of _CO2 was calculated with errors smaller than 0.1 ^cm-1 (= 0.001 kJ / mol) It was shown that the level energy of the Fermi resonance level of CO2 can be calculated with errors smaller than 0.1 cm-1 (= 0.001 kJ/mol).

This study demonstrates that the quantum computer is a promising tool for calculating accurate vibrational energy levels of polyatomic molecules, which is needed in vibrational spectroscopy.

 

Announcement

Research Background
Quantum computers are expected to be extremely useful computing devices in the future in the fields of materials science and applied chemistry because of their potential to calculate the energy levels of molecules with large sizes, which are difficult to handle even with current supercomputers. However, currently available quantum computers suffer from errors in quantum computation due to many types of noise arising from interactions with the environment. Therefore, it is necessary to introduce methods to reduce the effects of noise (error suppression methods) in order to extract meaningful results from computations performed on a quantum computer. Currently, quantum computing research is in the process of developing algorithms for performing calculations on larger quantum computers in the future, and these algorithms are being verified using currently available quantum computers. What is important now is to develop effective methods to mitigate the effects of noise that is inevitably present in quantum computers. And the subject of research in quantum computer-based computation is how to deal with both statistical and systematic errors in the results of repeated calculations.

In vibrational spectroscopy, the vibrational energy levels of molecules are determined experimentally, and at the same time, their dynamical behavior on intramolecular potentials and potential surfaces are studied by theoretical methods. In general, calculating the energies of all vibrational levels of a polyatomic molecule is a very difficult problem, even with a supercomputer, because the memory required to handle multidimensional vibrational wave functions is too large. Therefore, it has been expected that quantum computers would be useful for the calculation of vibrational energy levels of molecules that cannot be handled by conventional classical computers, but a demonstration of the calculation of molecular vibrational energy levels using an existing quantum computer was not published until our 2021 publication (E. Lö A 103, 062609 (2021)).

In this study, the vibrational energy levels of _{CO2 molecules} were calculated as a first step to efficiently calculate the vibrational energy levels of large molecules using a quantum computer. _CO2, a well-known molecule in global warming, is an interesting molecule from the viewpoint of vibrational spectroscopy because of the existence of Fermi resonances. We proposed a new method named the reduced multi-state contracted variational quantum eigensolver (RMC-VQE for short) method, which uses both a classical computer and a quantum computer, and We have calculated the energy of the Fermi resonance levels and constructed their wavefunctions on the quantum computer ibm_kawasaki (Figure 1).

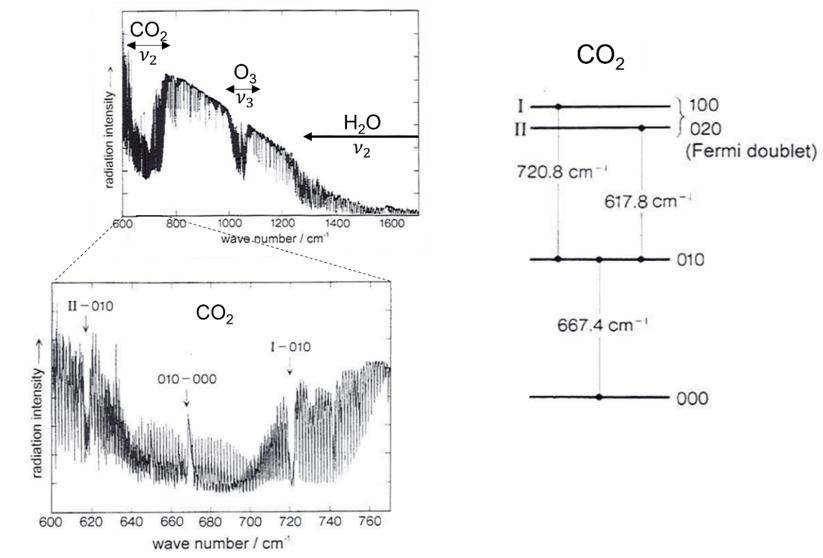
Figure 1: Measured Fermi resonance of _CO2 and related energy level diagram
Reproduced from K. Yamanouchi, "Quantum Mechanics of Molecular Structures," Springer-Verlag, Germany (2012).

 

Research Details
The RMC-VQE method calculates the Hamiltonian matrix ^{(Note 7)} by expressing the oscillatory wavefunction as a linear combination of two types of basis functions: a "classical" basis function system and a "quantum" basis function system. The matrix elements of the "classical" basis function system are constructed in such a way that even large molecules can be efficiently computed on a classical computer. Matrix elements involving "quantum" basis function systems are difficult for a classical computer to compute, but can be computed by a quantum computer. The vibrational energy is obtained by diagonalizing the Hamiltonian matrix ^{(Note 8)} in a classical computer. Thus, the quantum computer is used only for the computation of some important matrix elements that are difficult to compute with a classical computer. This approach reduces the effect of noise and at the same time allows more accurate calculation of vibrational energy levels than using only a classical computer.

For proof-of-principle purposes, the RMC-VQE method was applied to a two-mode model of _CO2 that takes into account symmetric stretching and angularly-inverted vibrations (see Figure 2(a)).

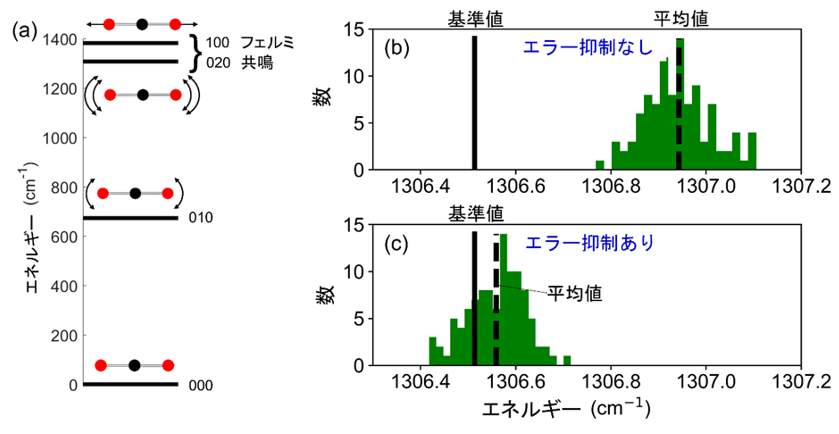
Figure 2: (a) Vibrational energy levels of the CO2 _molecule. (b) Energy histogram without error suppression (green) for one of the Fermi resonance levels calculated by ibm_kawasaki. (c) Energy histogram of the Fermi resonance state after error suppression (green).

 

In this case, the Hamiltonian matrix is sufficiently small that the exact reference energy level can be calculated by a classical computer. In this case, the Hamiltonian matrix of the simplified basis function system is calculated by both the quantum and classical computers for error suppression of the energy levels calculated by the quantum computer. The error can be estimated by comparing the energies obtained by the quantum computer and the classical computer.

Figure 2(b) and (c) show the vibrational energies obtained using four qubits in the ibm_kawasaki quantum computer. The energy histograms shown in Figures 2(b) and 2(c) were obtained by repeating the Hamiltonian matrix calculation and diagonalization 100 times. In Figure 2(b) without error suppression, the mean value has an error of about 0.5 ^cm-1 from the exact reference value, but in Figure 2(c) after error suppression, the mean value agrees well with the reference value.

 

Social Significance and Future Plans
By demonstrating that the vibrational energy levels of _CO2 can be calculated accurately, we have shown that quantum computers may be useful for vibrational spectroscopy. From now on, we will work on the calculation of vibrational energies of larger polyatomic molecules by using more qubits. In addition, the newly introduced RMC-VQE method is a general method that can be applied not only to the calculation of vibrational energy levels but also to the calculation of electronic energy levels of atoms and molecules.

 

Journals

Journal name	AVS Quantum Science
Title of paper	Evaluation of vibrational energies and wave functions of CO2 on a quantum computer
Authors	Erik Lötstedt*, Kaoru Yamanouchi*, and Yutaka Tachikawa
DOI number	https://doi.org/10.1116/5.0091144

 

Terminology

1 Algorithm

A clearly defined procedure for solving a particular problem as a combination of simple calculations or operations. ↑up

Note 2 Quantum computer

A computer built from quantum bits. Unlike classical computers, where the value of a bit takes only 0 or 1, a qubit can take on a superposition of 0 and 1 states. By utilizing the superposition of qubit states, it is expected to be able to simulate much larger molecules than conventional classical computers. ↑up

Note 3: Energy of vibrational levels

Since molecular vibration is described by quantum mechanics, the energy of vibrational motion can only take discrete values. The level is called the vibrational energy level, and its energy is called the energy of the vibrational level. In the field of vibrational spectroscopy, the vibrational energy level of a molecule is determined experimentally, and its dynamic behavior on a potential or potential surface within a molecule is determined by theoretical methods. ↑up

Note 4 Classical computer

A conventionally existing computer, such as a PC, supercomputer, or smartphone. ↑up

Note 5 ibm_kawasaki

IBM Quantum System One, a 27-qubit quantum computer by IBM Corporation. The qubits are made of superconducting electronic circuits controlled by microwave pulses. ibm_kawasaki was installed in 2021 at the "Souzou no Mori Kawasaki New Industry Creation Center" in Shin-Kawasaki. ↑up

Note 6 Fermi resonance level

Two vibrational energy levels of _CO2 with a spacing of 103 ^cm-1. This small split was described by Enrico Fermi in 1931 as the result of the mixing of a single excited state of a symmetric stretching vibrational mode and a doubly excited state of an angular vibrational mode. ↑up

Note 7 Hamiltonian matrix

A matrix containing information about the energy levels of a quantum mechanical system. Level energies are obtained by diagonalizing the Hamiltonian matrix ( ^{see(Note 8))}. ↑up

Note 8 Diagonalization

A numerical procedure to obtain the eigenvalues of a matrix. After appropriate similarity transformation of the matrix, the matrix becomes a diagonal matrix with eigenvalues as diagonal matrix elements. ↑