Ryuhei Yoshida (Department of Chemistry, 1st year, Master's course)

Erik Lötstedt, Associate Professor, Department of Chemistry

Kaoru Yamauchi, Professor, Department of Chemistry

 

Key points of the presentation

• Hückel molecular orbitals ^{(Note 1)} By representing the matrix elements of the Hamiltonian using quantum gates ^{(Note 2)}, the orbital energies of the molecular orbitals of basic π-electron molecules such as ethylene and benzene were calculated using the quantum computer ibm_kawasaki ^{(Note 3)}.
• We have shown that orbital energies can be obtained with high accuracy and precision by incorporating the simplest error suppression ^{(Note 4)} method, which is to discard physically meaningless states generated by errors in quantum calculations.
• The developed method is so general that it provides a guideline for the instantaneous determination of electronic states of large π-conjugated systems such as fullerenes, graphene, and carbon nanotubes by a quantum computer.

 

Summary of Presentation

Now that quantum computing is becoming a reality, it is needless to say that it is important to develop quantum technology in terms of hardware to "minimize the occurrence of errors, which are currently unavoidable in quantum computation. At the same time, however, there is an urgent need to provide guidance on the problems of "how to construct efficient quantum circuits for computing the target system" and "how to correct errors in the results of calculations using these quantum circuits to predict more correct values.

Associate Professor Lötstedt, Professor Yamauchi and their research group at the Graduate School of Science, The University of Tokyo, have launched the "Applied Quantum Chemistry with Qubit (AQUABIT)" project ( https://www.utokyo.ac.jp/adm/fsi/en ) with support from DIC Corporation under the Quantum Initiative at The University of Tokyo. /adm/fsi/en/projects/quantum/project_00064.html) with the support of DIC Corporation, and has been working on the "development of a methodology to calculate molecular systems using a quantum computer" and the "improvement of calculation accuracy by error suppression of calculation results using a quantum computer.

In this study, as a part of these efforts, molecular orbitals were calculated for ethylene, cyclopropene, cyclobutadiene, 1,3-butadiene, and benzene by the Hückel molecular orbital method, which is the most basic method for calculating electronic states of molecules, using the quantum computer, ibm_kawasaki. It was shown that the orbital energies can be obtained with high accuracy and precision if the simplest error suppression, i.e., discarding "physically meaningless states" generated by quantum calculation errors, is applied.

Both "expansion of orbital functions by basis functions" and "description of Hamiltonian matrices by quantum circuits" are versatile, and the results of this study are expected to be utilized for quantum calculations of electronic states of large pi-conjugated systems such as fullerenes, graphene, and carbon nanotubes in the future.

 

Announcement

The Hamiltonian by the Hückel molecular orbital method can be written as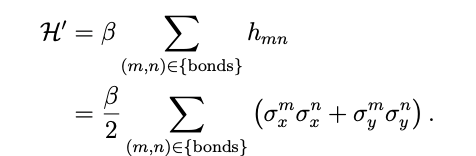

The Hamiltonian by the Hückel molecular orbital method can be written as where β is the resonance integral, m and n represent the numbers of carbon atoms, and both indicate that the Pauli operator acts on the i-th and j-th qubits, respectively.

Therefore, by introducing the operator _Ur for efficient computation by a quantum computer, the Hamiltonian is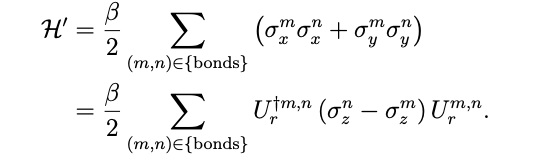

denote the Hamiltonian.

The energy of the kth excited orbital is then obtained by finding the energy of each π-bond and adding it, using the kth basis function and the excitation operator that converts it to an orbital
It can be written as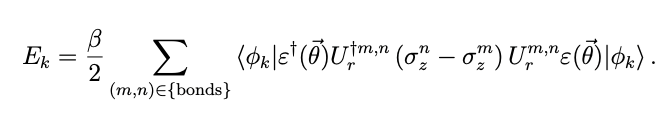
. Thus, all orbital energies can be described using quantum gates in a way that minimizes the number of CNOT gates.

For example, the quantum circuit for finding the energy of the ground state at the π bond between the 0th and 1st carbon atoms in cyclobutadiene ( _C4H4 ) in (Figure 1)(c) can be expressed as in the next section.

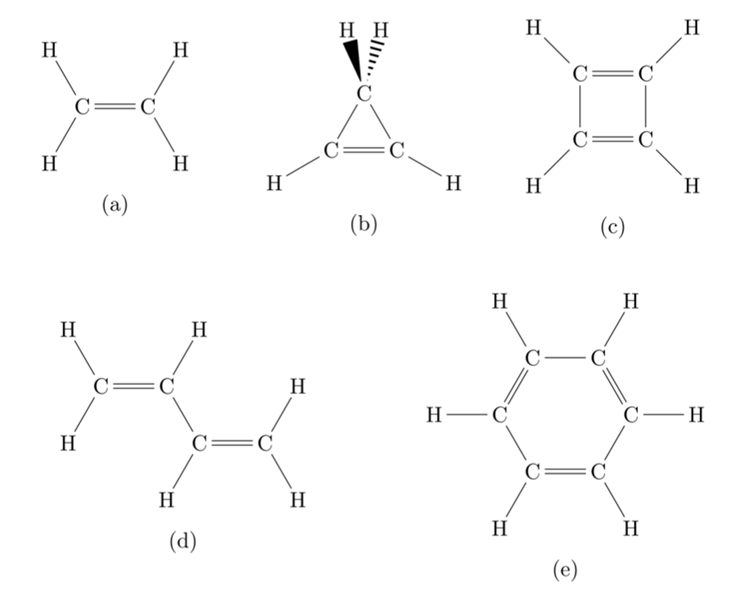
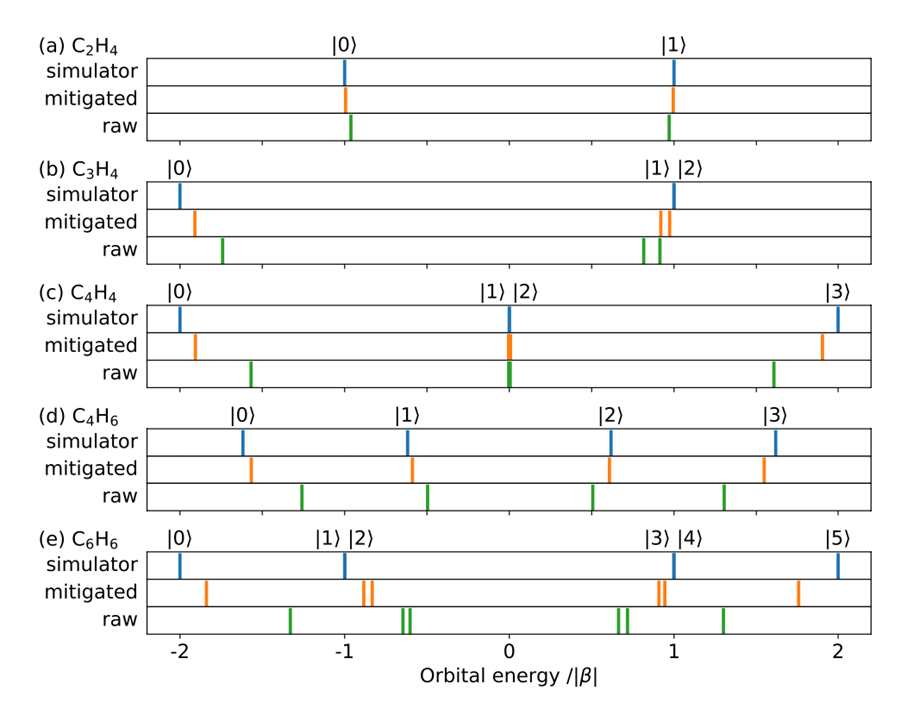
Figure 1: Five types of π-electron molecules whose orbital energies were obtained by the quantum computer ibm_kawasaki.
(a) Ethylene (ethylene) _C2H4
(b) cyclopropane _C3H4
(c) cyclobutadiene _C4H4
(d) 1,3-butadiene _C4H6
(e) benzene _C6H6

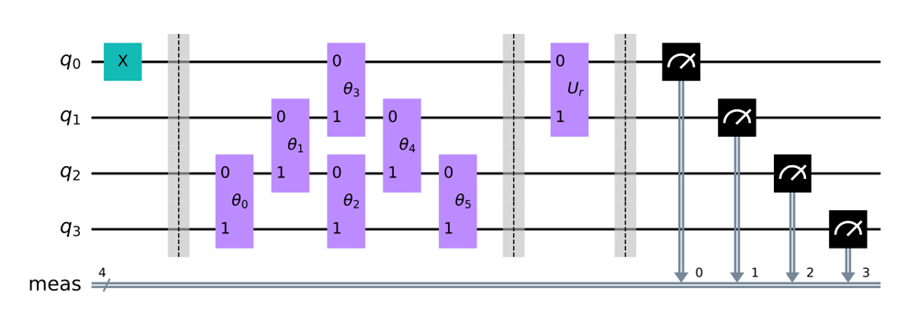
Here, each vertical rectangle represents an operation, and the three vertical dotted lines are for convenience in clarifying the meaning of the quantum circuit. On the left side of the leftmost vertical dotted line, a basis function is provided, between the first and second dotted lines from the left represent operations with excitation operators, and between the second and third dotted lines from the left represent operations with _Ur.

Such a quantum circuit was computed using a quantum computer, and the results were then organized using a classical computer. In fact, in the quantum circuit introduced as above, the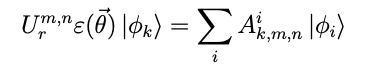

The square of the absolute value of the amplitude , expressed as In this case, the orbital energy is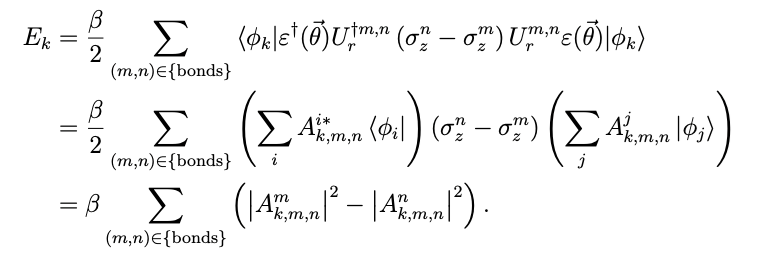

is given by using the square of the absolute value of , as shown in Fig. 1.

Therefore, the energies of the molecular orbitals were obtained by using the | | calculated for each bond by the quantum computer, and by performing only the addition and subtraction of these energies by the classical computer.

（The orbital energies calculated using ibm_kawasaki for the five types of π-electron molecules (Figure 1) are shown in the raw rows of the following figure. For comparison, the simulator values, which are the same as the exact solutions without statistical errors or quantum computer errors, are shown in the simulator row.

In addition, the mitigated row shows the results of the ibm_kawasaki calculation with error suppression. It is shown that the calculation results are greatly improved by error suppression. For example, for the basis energy of benzene, the result without error suppression is α-1. 3|β|, which is far from the correct value α-2|β|, but with error suppression using ibm_kawasaki, α-1. 8|& beta; |, indicating that it is possible to obtain orbital energies closer to the correct values.

 

Journal

Journal name	The Journal of Chemical Physics
Title of paper	Quantum computing of Hückel molecular orbitals of pi-electron systems
Author(s)	Ryuhei Yoshida, Erik Lötstedt, Kaoru Yamanouchi*, Ryuhei Yoshida
DOI Number	10.1063/5.0086489

 

Terminology

1 Hückel molecular orbital

A molecular orbital method proposed by Hückel in 1930. It can describe the molecular orbitals of pi-conjugated molecules and their energies. The molecular orbital is a superposition of atomic orbitals of carbon atoms, and only one p-orbital per carbon atom is considered. The values of Coulomb integral and resonance integral are assumed to be the same in the molecule as α and β, respectively. ↑up

Note 2 Quantum gate

The smallest unit of operation in a quantum computer, corresponding to the AND, OR, XOR, NOT gate, etc. in a classical computer. A gate that acts on only one qubit is called a single-qubit gate, and a gate that acts on two qubits is called a two-qubit gate. In many types of quantum computers, including superconducting quantum computers, two-qubit gates are known to be overwhelmingly noisier than single-qubit gates. ↑up

Note 3 Quantum computer ibm_kawasaki

A computer that performs calculations based on the superposition of a computational basis of 0s and 1s, called a quantum state, based on quantum mechanics. The ibm_kawasaki is a superconducting quantum computer with 27 qubits, which was introduced to The University of Tokyo last year in 2021. ↑up

Note 4 Error Suppression

A method to correct errors in quantum gate operations. In addition to a method that discards states that physically cannot exist, there is a method called Clifford data regression that improves results by comparing them with the results of quantum circuits that can be efficiently simulated by a classical computer, and a method called zero noise extrapolation that reduces noise in the two-qubit gate with the highest error rate. A technique called zero noise extrapolation, which reduces the noise in the two-qubit gate with the highest error rate, is also known. ↑up