DATE2022.02.17 #Press Releases
First Discovery of Antiferromagnetic Exciton Insulators
Disclaimer: machine translated by DeepL which may contain errors.
Hidemaro Suwa (Assistant Professor, Department of Physics)
Points of presentation
- We have newly discovered antiferromagnetic exciton insulators produced by excitons, which are bound states of electrons and holes, both experimentally and theoretically.
- The existence of antiferromagnetic exciton insulators produced by spin triplet excitons has been clarified.
- The role of charge, spin, and orbital degrees of freedom of electrons in antiferromagnetic exciton insulators will be clarified in the future, leading to the design and application of quantum materials.
Summary of Presentation
Assistant Professor Suwa, Graduate School of Science, The University of Tokyo, in collaboration with research groups from Brookhaven National Laboratory, Paul Scherrer Institute, University of Tennessee, Argonne National Laboratory, Oak Ridge National Laboratory, Chinese Academy of Sciences, and Shanghai University of Science and Technology, has discovered a new antiferromagnetic exciton insulator produced by the electron-hole coupling state from both experimental and theoretical The new discovery was made both experimentally and theoretically.
Just as a pair of electrons in a material undergoes a phenomenon called Bose-Einstein condensation (Note 1) to produce a superconductor, an exciton, which is a bound state of an electron and a hole, condenses to produce a state called an exciton insulator. Focusing on the quantum mechanical properties of excitons, exciton insulators produced by condensation of excitons in the spin singlet (Note 2 ) have been studied intensively, but materials in which excitons in the spin triplet are condensed have not been found. From resonant inelastic x-ray scattering (Note 3 ) experiments and theoretical calculations on iridium oxide Sr3Ir2O7, the research group has revealed that it is an antiferromagnetic exciton insulator with condensed triplet excitons.
In the future, experimental verification and manipulation of the Bose-Einstein condensation phenomenon of triplet excitons will be possible. The role of charge, spin, and orbital degrees of freedom of electrons in antiferromagnetic exciton insulators will be further clarified, leading to the design and application of quantum materials.
Announcement
When an electron and a hole (hole) form a bound state in a material, they behave as a composite particle called an exciton. Just as electron pairs produce superconductors, excitons produce a state called exciton insulators when they undergo Bose-Einstein condensation. Although this phenomenon has long been predicted theoretically, it is not easy to identify exciton insulators in real materials. Focusing on the quantum mechanical properties of excitons, exciton insulators produced by the condensation of spin-singlet excitons have been studied intensively, but no material in which spin-triplet excitons condense has been found. The reason is that condensation of triplet excitons requires both a special crystal structure and an exquisite interaction balance.
One of the states that arise from the condensation of triplet excitons is the antiferromagnetic exciton insulator. The research group has revealed that this state arises by the following mechanism. First, hypothetically assume a physical system in which the spin-orbit coupling (Note 4 ) and the repulsive Coulomb interaction between electrons are neglected and the system becomes a metal with no charge gap. Then we consider a material in which spin-orbit coupling is added and band hybridization occurs, resulting in a nonmagnetic band insulator with a small charge gap. In this situation, the triplet state is stabilized by considering repulsive interactions between electrons. This is because, due to the nature of Fermi particles (Note 5), the electron pairs in the triplet are further apart from each other than in the singlet. Describing this effect in terms of holes, which are "holes" in electrons, means that there is an effective attraction between electrons and holes. As the electron-electron interaction is further strengthened and the quantum critical point (Note 6) is reached, the exciton binding energy finally becomes larger than the charge gap, the band insulator becomes unstable, and the exciton undergoes Bose-Einstein condensation (Figure 1). After this critical point, an antiferromagnetic exciton insulator with alternating spin up and spin down magnetic ordering is produced.
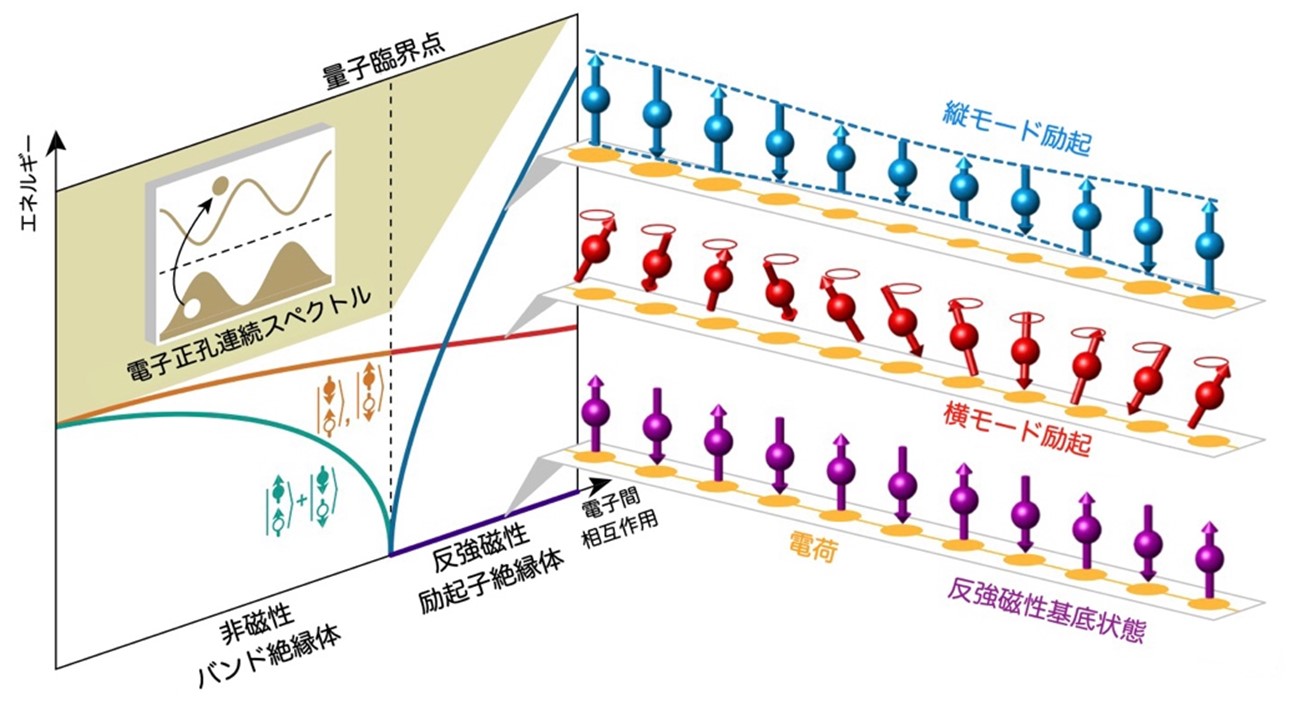
Figure 1: Dependence of excitation energy on electron-electron interaction and excitation modes of antiferromagnetic exciton insulators. When electron-electron interactions are taken into account in a nonmagnetic band insulator, the exciton, a bound state of electrons and holes, stabilizes and separates from the electron-hole continuum spectrum that extends into the high-energy region. Here, the easy-axis anisotropy of the spin interaction splits the exciton into two energies. As the electron interaction is intensified, the higher energy of the two excitons results in transverse mode excitations in antiferromagnetic exciton insulators. On the other hand, low energy excitations become zero at the quantum critical point and then become longitudinal mode excitations in the antiferromagnetic exciton insulator. These longitudinal mode excitations are coupled to the charge degrees of freedom and oscillate the spin length, which is a characteristic excitation.
The key to identifying antiferromagnetic exciton insulators is to detect the characteristic excitation modes, called longitudinal modes. In antiferromagnets, there is generally a transverse mode of excitation called magnon (Note 7), but in antiferromagnetic exciton insulators, in addition, a longitudinal mode appears in which the spin length (on average) expands and contracts. If the condition that the excitation energy of the longitudinal mode is less than twice the energy of the transverse mode is satisfied, a pronounced response from the longitudinal mode can be detected. If this condition is not met, the longitudinal mode splits into two transverse modes, and the longitudinal mode-derived spectral peak is lost. To satisfy the condition, the spin interaction must have easy-axis anisotropy (Note 8 ) and the excitation energy of the transverse mode must be finite, and the excitation energy of the longitudinal mode must be sufficiently small that the system is close to the quantum critical point.
The research group has found that the iridium oxide Sr3Ir2O7 is an antiferromagnetic exciton insulator that satisfies the above conditions. They have also theoretically predicted the longitudinal mode features of this material and experimentally identified them using resonant inelastic x-ray scattering. In the crystal, one electron is placed on average in an electron orbital with iridium due to the effect of strong spin-orbit coupling. In addition, the crystal structure consists of two overlapping layers containing iridium, forming a quasi-two-dimensional system (Figure 2).
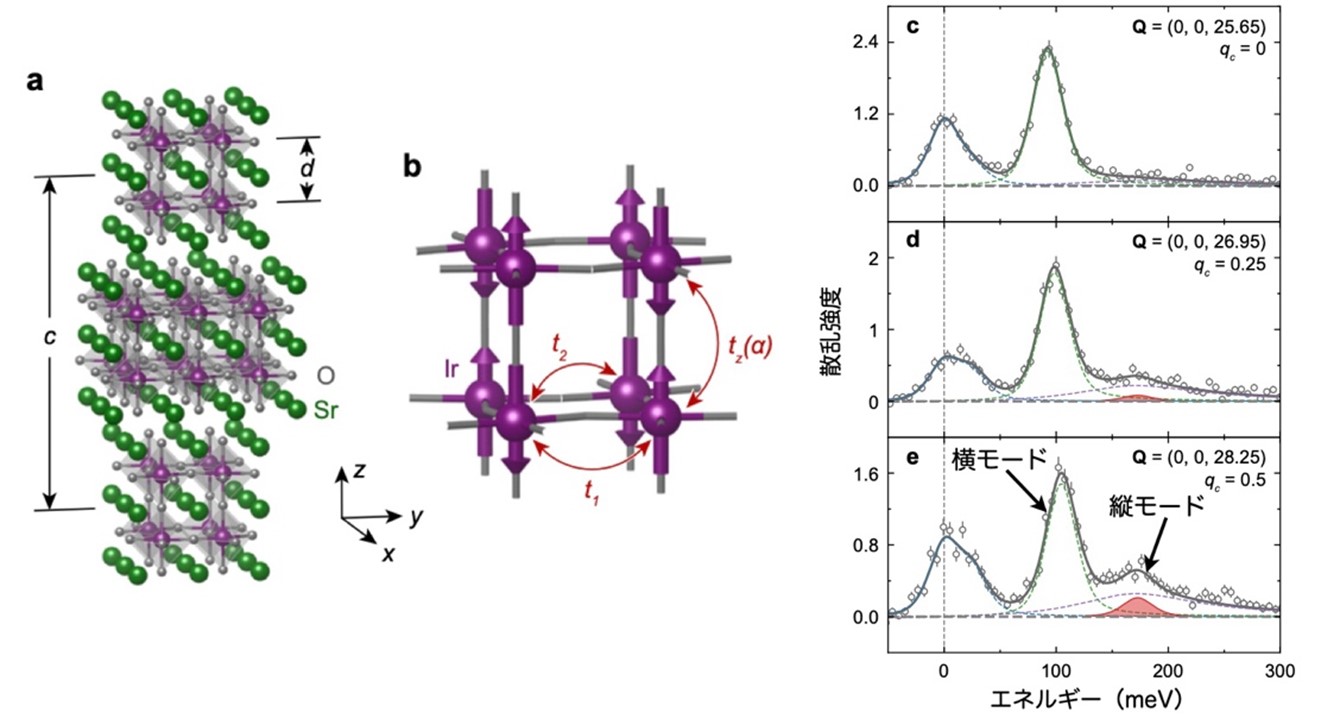
Figure 2: (a) Crystal structure of iridium oxide Sr3Ir2O7. The iridium-containing layers are stacked in the z direction, overlapping two layers each. (b) Iridium in two layers and antiferromagnetic ordering in the z direction. (c) Energy dependence of the scattering intensity at wavenumbers of qc = 0, (d) qc = 0.25, and (e) qc = 0.5. The longitudinal mode, indicated by the red peak, does not appear for qc = 0 and shows maximum intensity at qc = 0.5.
Due to the conservation of the sum of the longitudinal (z) components of the spin in this material, no bound state is formed when the phases of the two layers are aligned. Therefore, longitudinal modes do not emerge at wavenumber vectors where the two layers are in phase ( qc = 0), and the scattering intensity of longitudinal modes is maximized at wavenumbers where the phases are opposite ( qc = 0.5). Also, reflecting the fact that the charge gap and magnetic excitation energy are comparable, the peak of longitudinal mode excitation appears only at a limited number of wavenumber vectors. A group at the University of Tokyo led the theoretical calculation and succeeded in reproducing the experimental results with high accuracy (Figure 3).
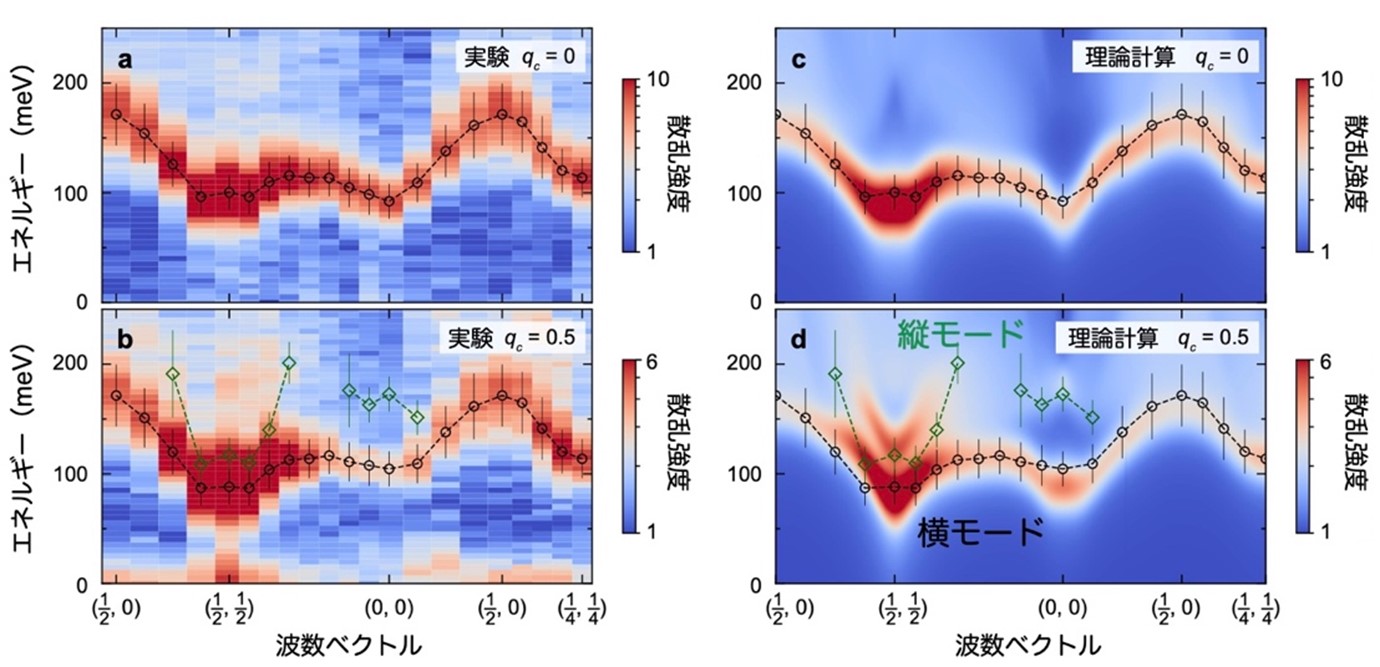
Figure 3: Color plot of scattering intensity versus wavenumber vector and energy. The black plot shows the peak position of the transverse mode observed experimentally, and the green plot shows the peak position of the longitudinal mode observed experimentally. Transverse modes appear over the entire wavenumber vector, whereas longitudinal modes are dispersed in the electron-hole continuum spectrum at high energies and therefore appear only in a limited number of wavenumber vectors.
Furthermore, the temperature dependence of longitudinal mode excitation energy shows a significant decrease (softening) near the magnetic transition temperature (Figure 4). This is consistent with the theoretical prediction that excitons that begin to stabilize at temperatures above the transition temperature undergo Bose-Einstein condensation at the phase transition temperature. Also, reflecting charge-spin coupling, electrical resistance increases with decreasing carriers at the magnetic transition temperature. These phenomena could not be understood in a unified manner by previous theories based on the spin model. The research group developed a theory that appropriately incorporates the charge degrees of freedom and succeeded in identifying an antiferromagnetic exciton insulator while comprehensively explaining the experimental results for Sr3Ir2O7.
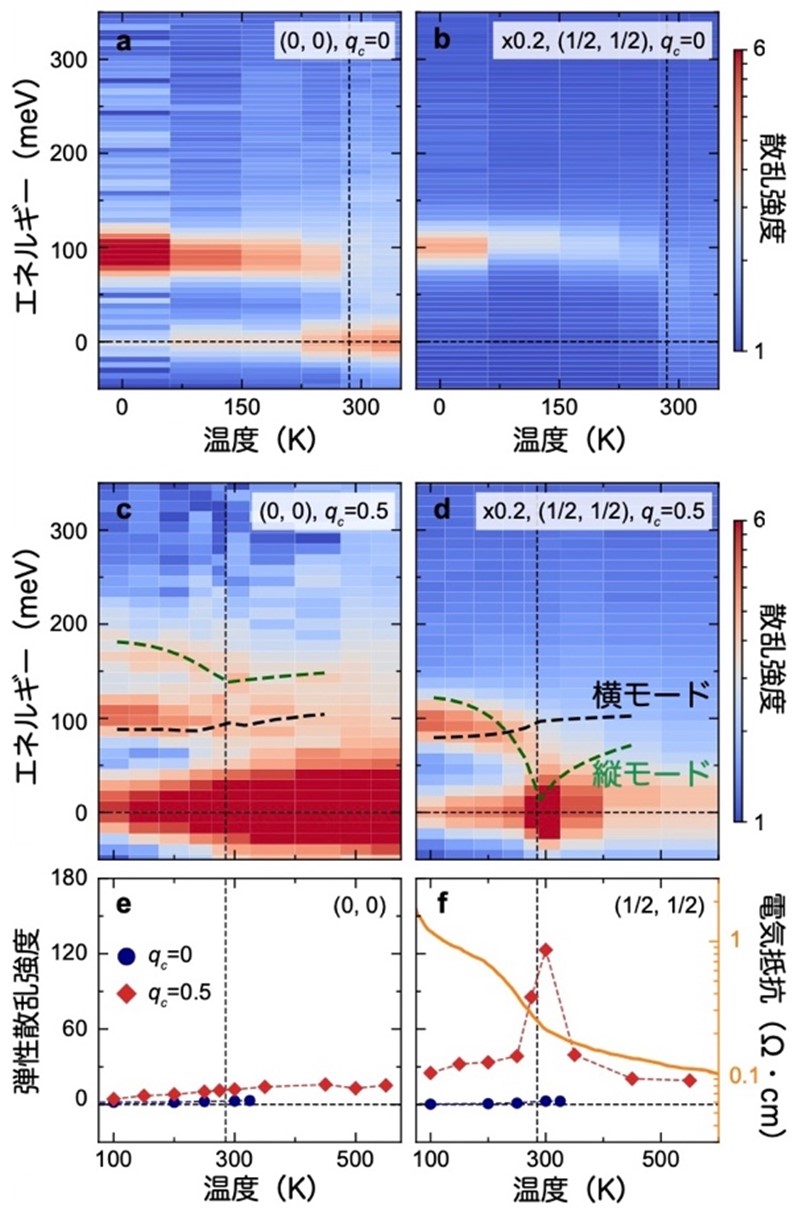
Figure 4: Color plots of scattering intensity versus temperature and energy for (a) wavenumbers (0, 0) and qc = 0, (b) (1/2, 1/2) and qc = 0, (c) (0, 0) and qc = 0.5, (d) (1/2, 1/2) and qc = 0.5. The dashed lines in (c) and (d) indicate the peak positions of the transverse (black) and longitudinal (green) modes obtained from theoretical calculations. (e) Temperature dependence of elastic scattering intensity near zero scattering energy at wavenumbers (0, 0) and (f) (1/2, 1/2). The elastic scattering intensity at wavenumbers (1/2, 1/2) and qc = 0.5 shows a prominent peak near the magnetic transition temperature (285 K), suggesting exciton Bose-Einstein condensation. Also, due to charge-spin coupling, the electrical resistivity increases with the magnetic transition.
The discovery of the long-discovered antiferromagnetic exciton insulator will allow more detailed experimental verification and manipulation of triplet exciton condensation phenomena in the future. This achievement is expected to lead to the scientific elucidation of physical phenomena involving the complex interplay of charge, spin, and orbital degrees of freedom of electrons, as well as to the design and engineering applications of quantum materials in the future.
Journal
-
Journal name Nature CommunicationsTitle of paper Antiferromagnetic excitonic insulator state in Sr3Ir2O7Author(s) D. G. Mazzone*, Y. Shen*, H. Suwa*, G. Fabbris, J. Yang, S-S. Zhang, H. Miao, J. Sears, Ke Jia, Y. G. Shi, M. H. Upton, D. M. Casa, X. Liu, J. Liu, C. D. Batista, M. P. M. Dean*.DOI Number
Terminology
1 Bose-Einstein condensation
A phenomenon in which a very large number (macroscopic number) of Bose particles take the same single-particle state. When it occurs in matter, it produces interesting quantum states such as superconductors, superfluids, and exciton insulators. ↑up
Note 2: Singlet and Triplet
The singlet is a quantum mechanical state with zero spin and has one state, while the triplet is a state with one spin and has three states. spin anisotropy causes the energy of the three states of the triplet to split. ↑up
Note 3 Resonant inelastic x-ray scattering
An experimental technique to observe the energy and momentum (wavenumber) of excitation by spectroscopy of scattered X-rays generated in the process of resonant excitation of inner-shell electrons by incident X-rays and relaxation of the excited state. ↑up
Note 4 Spin-orbit coupling
Interaction between electron spin and orbital angular momentum arising from relativistic effects. ↑up
Note 5 Properties of Fermi particles
The property that the sign of the total wavefunction reverses with respect to the exchange of two homogeneous Fermi particles. Since the spin-triplet electron pair is spin symmetric with respect to the exchange, the sign of the wavefunction in the real space part is inverted. As a result, the electron pairs in the triplet are further apart from each other than in the singlet. ↑up
Note 6 Quantum critical point
A phase transition point caused by quantum fluctuations at absolute temperature. Various physical quantities behave in a power-law (critical) manner with respect to distance and time. ↑up
Note 7 Magnon
A virtual particle describing the excitation of spin waves arising from a magnetically ordered state. Formulates magnetic excitations of transverse modes. ↑up
Note 8 easy-axis anisotropy
A property in which one axial direction is preferred over another. In a magnetically ordered state, the spins are aligned along the preferred axis (easy axis). ↑up


