DATE2021.10.21 #Press Releases
Theoretical investigation of surface states and novel transport phenomena of
magnons in magnetic insulators where electrons cannot move.
Disclaimer: machine translated by DeepL which may contain errors.
Hiroki Kondo (Department of Physics, 3rd year of Doctoral program)
Yutaka Akagi (Assistant Professor, Department of Physics)
Points of the presentation
- We have proposed a model in which a special state of magnon, a particle responsible for transport in magnetic materials, appears on the surface, originating from the nontrivial topology of quantum mechanical wavefunctions (Note 1).
- This surface state has properties such as the massless Dirac particle (Note 2), spin polarization that changes the direction of spin carried by magnons depending on the direction of motion, and electric field response of magnons without electric charge, which can be a treasure house of novel properties in magnetic materials.
- It is expected that the above surface state of magnons will appear in van der Waals magnets such as CrI3(Note 3).
Summary of presentation
In a crystal with periodically arranged atoms, if the spins corresponding to the rotational motion of electrons, which are the bearers of magnetism, are regularly aligned, the material is called magnetic. Even in insulators, where the electrons themselves cannot move around, the "motion" of the spins governs the properties of the magnetic body. In particular, heat and other conduction phenomena in magnetic insulators are carried by spin waves (Fig. 1), in which the inclination of the spins from the aligned direction is transmitted like a wave.

Figure 1: Spin wave. In a magnetic material with aligned spins in the upward direction, conduction phenomena such as heat can be described by a picture in which the displacement of spins slightly inclined from the top is transmitted as a wave. In quantum mechanics, such a wave can be regarded as a particle at the same time, and that particle is a magnon.
The elementary excitation of this spin wave can be described as a particle by the language of quantum mechanics, and that particle is called a magnon. In recent years, much research has been conducted on nontrivial transport phenomena due to magnons under various symmetries, but many theoretical models proposed have had a tenuous connection with real matter.
Hiroki Kondo, graduate student, and Hiroshi Akagi, Assistant Professor, Graduate School of Science, The University of Tokyo, theoretically proposed a magnetic model in which magnons with a massless Dirac particle-like dispersion appear on the surface of a magnetic material, originating from the nontrivial topology of the magnon wavefunction, and pointed out that it is realized in a van der Waals magnetic material, CrI3 I pointed out that it can be realized in the van der Waals magnet CrI3. This topological magnon crystal insulator is naturally realized by a symmetry that combines not only the magnetic symmetry with respect to spin but also the spatial symmetry of the crystal. Magnons in such a magnetic body show an unusual response to electric fields and can be a treasure trove of novel physical properties.
Contents of presentation
Background of Research
In recent years, quantum materials have been increasingly studied in the field of condensed matter physics, and topological insulators have attracted a great deal of attention. Topological insulators are materials in which a "metallic" state appears on the surface/edge of the insulator due to the nontrivial topology of the electron wavefunction in the material. The electrons in this "metallic" state exhibit interesting properties, such as one-way flow on the surface, and this is the setting for many phenomena not seen in conventional materials. In particular, when realized in three-dimensional matter, the "metallic" state appears on the surface ( two-dimensional ), but due to the large degrees of freedom, it exhibits more diverse properties than the one-dimensional edge state in two-dimensional matter.
The study of topological properties in such electron systems has also extended to Bose particle (Note 4) systems, and in particular, topological properties of magnons, which are fundamental quasiparticles (Bose particles) in magnetic materials, have been actively studied in recent years. A typical example is the topological thermal Hall effect, in which heat flow and temperature gradients are generated in the direction perpendicular to the applied temperature gradient (and magnetic field). An important role here is played by the Jarosinski-Moriya interaction, which appears when the spatial inversion symmetry of the crystal is broken, shifting and twisting the direction of neighboring spins. This interaction makes the structure of the magnon wavefunction nontrivial in terms of topology, and the special surface states described above also appear in magnon systems.
On the other hand, the magnon/Bose particle system encompasses the non-Hermitian (Note 5) property, and its theoretical development is non-trivial due to its peculiar mathematical properties. The recent explosion of research on topological properties was triggered by the proposal of topological insulators of electron systems protected by time-reversal symmetry, but the Kramers' theorem (Note 6), which plays an essential role here, is not directly applicable to Bose particle systems, and most of the research on their topological phases has not been conducted. Most of the studies on its topological phase were limited to discussions on systems without time-reversal symmetry. One step further, effective time-reversal symmetry in magnon systems was also introduced, but to satisfy it in a three-dimensional system, an artificial model of a magnetic body had to be considered.
Our Research
We focused on the fact that the Kramers' theorem can be applied to magnon systems if it is symmetric with respect to the time reversal (reversal of spin direction) in the magnetic body and the translational operation of half the unit cell of the crystal (half the period of the crystal). This symmetry is satisfied under very natural circumstances, such as when the layers of a stacked magnetic material are bound together under spin-spin interactions such that the spins want to face in opposite directions. In this study, we proposed a theoretical model in which a special surface state of magnons appears in a magnetic material with a honeycomb lattice stacking structure (Figure 2).

Figure 2: Model of the proposed magnetic material. The structure resembles a stacked honeycomb lattice. The arrows indicate the spin direction of the atoms in the lattice. When ferromagnetic interactions (neighboring spins going in the same direction) work within the layers of the honeycomb lattice and antiferromagnetic interactions (neighboring spins going in the opposite direction) work between the layers, the spins align in the direction as shown in the figure. Such a magnetic body is symmetric with respect to the combined operation of time reversal and translation by one layer, which corresponds to a reversal of spin orientation.
Because of their nontrivial topology and their connection to crystal symmetry, these magnetic materials should also be called topological magnon crystal insulators. In particular, the proposed model of magnetic materials is expected to be realized in van der Waals magnetic materials such as CrI3. In the case of CrI3 with a stacking structure called monoclinic structure (monoclinic system), we investigated this model with respect to the parameters of the model estimated by density functional theory (Note 7) and other methods, and found that the above special surface state appears.
This surface state has a linear dispersion like a massless Dirac particle, and exhibits interesting properties such as the spin direction carried by the magnon changing depending on the direction of motion. In order to extract new physical properties derived from this property, we considered the electric field response to magnons without charge. It is known that the Jarosinski-Moriya interaction changes when an electric field is applied to a magnetic material, changing the position of ions and other elements in the crystal. The effect it has on the magnon wave function can also be interpreted as an addition of a complex exponential factor derived from the electric field, the Aharonov-Casher effect (Note 8). Considering this contribution, we found that the Dirac dispersion of the magnon surface states on the magnetic surfaces facing each other shifts upward and downward, respectively (Figure 3).
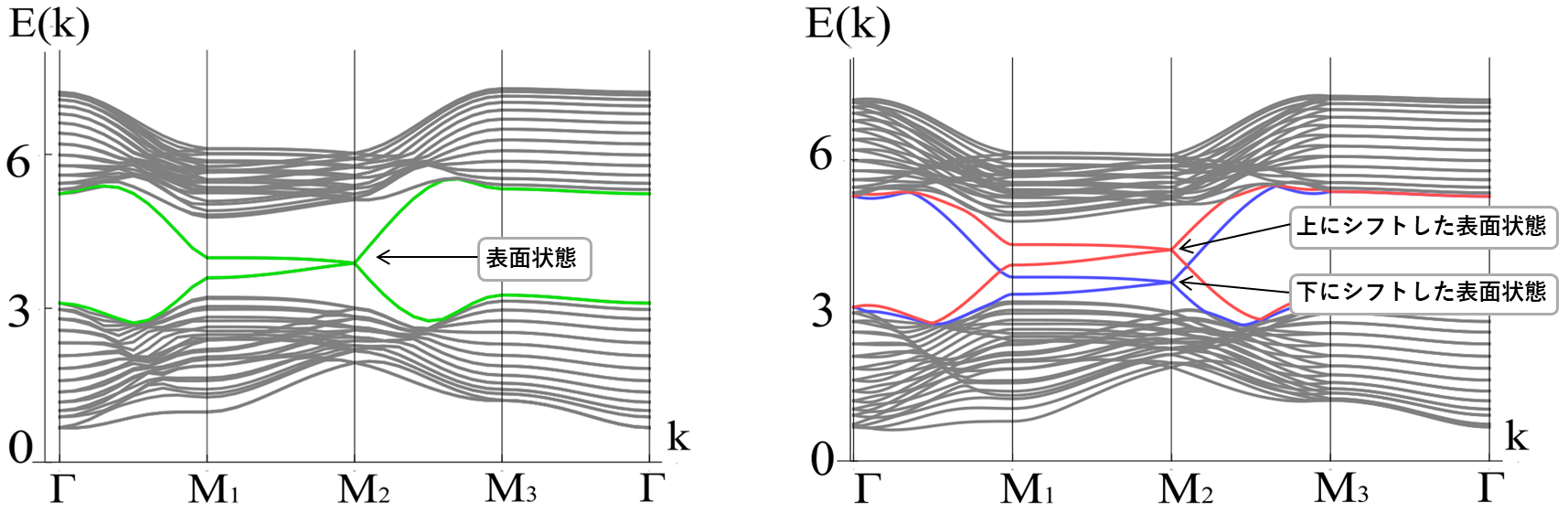
Figure 3: (Left) Magnon band structure (momentum vs. energy) in the above magnetic materials. The line straddling the two bundled upper and lower bands is the surface state, and the Dirac-type linear dispersion appears at the M2 point.
(Right) Magnon band structure when an electric field is applied. Before the electric field was applied, the bands overlapped on the two surfaces facing each other, but the electric field shifted one band up and the other band down.
This causes an increase/decrease in the number of magnons on each surface, resulting in a magnon flow (Fig. 4). This electric field response by magnons without charge is a qualitatively new transport phenomenon that has no counterpart in electronic systems.
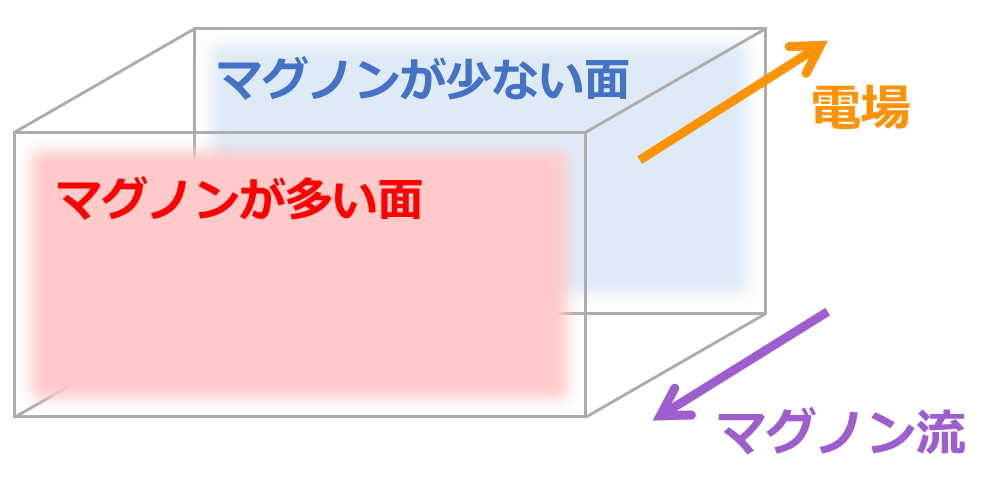
Figure 4: When an electric field is applied, the number of magnons increases on the front surface, where the band structure has shifted upward in Figure 3, and decreases on the back surface, where it has shifted downward. The magnons accordingly flow in the direction shown in the figure.
Future Prospects
Magnon states protected by the time-reversal × translation symmetry proposed in this study not only appear on the surface but also exhibit a variety of physical properties, such as having Dirac-type linear dispersion, spin polarization dependent on the direction of motion, and a special electric field response. In addition to the electric field response considered in this study, many other novel physical properties are expected to be latent. This research proposal opens up the possibility of novel physical properties and transport phenomena by magnons in magnetic insulators, where electrons cannot move. In the future, we plan to develop our research for experimental observation and demonstration, as well as to explore related novel physical properties.
Journal
-
Journal name Physical Review Letters Title of paper Dirac surface states in magnonic analogs of topological crystalline insulatorsAuthors Hiroki Kondo* and Yutaka AkagiDOI Number 10.1103/PhysRevLett.127.177201 URL https://link.aps.org/doi/10.1103/PhysRevLett.127.177201
Terminology
Note 1 Topology
A branch of mathematics that investigates geometric properties that are invariant with respect to continuous deformations (deformations that do not cut or attach). For example, it asserts that a coffee cup and a donut have the same shape. ↑ up
Note 2 Dirac particle
In the framework of relativistic quantum mechanics, particles moving at nearly the speed of light are described by the Dirac equation. In particular, in the case of photons, which are massless, their energy is linear with respect to their momentum. Particles flowing in solids, such as electrons in graphene, can behave as effectively massless particles, and such particles are generally called Dirac particles in the field of condensed matter physics. ↑ up
Note 3 Van der Waals magnetism
A magnetic body in which layers of atoms are stacked and bound together by van der Waals forces. ↑ up
Note 4 Fermi particles/Bose particles
Some particles in the natural world have wavefunctions whose signs, when described by quantum mechanics, are reversed by the exchange of particles, while others do not. The former are called Fermi particles and the latter are called Bose particles. The electron is a typical example of a Fermi particle, and photons and magnons are typical examples of Bose particles. ↑ up
Note 5 Non-Hermitian
The operators involved in observables in quantum mechanics are generally represented as Hermitian matrices. Hermitian means that the complex transpose (Hermitian conjugate) is equal to itself. In recent years, physics in non-Hermitian systems that do not satisfy Hermitianity, such as quantum systems under measurement and open quantum systems, have been actively studied beyond this framework. ↑ up
Note 6: Kramers' theorem.
The theorem states that if an interaction-free Fermi-particle system (or a system consisting of an odd number of Fermi-particles) has time-reversal symmetry, there exist degenerate (equal energy) states of energy linked by time reversal. ↑ up
Note 7 Density functional theory
A method of obtaining electronic states at a lower numerical cost by considering the electron density (functional theory) instead of the wavefunction in quantum mechanics and reducing it to the equation for the case without interaction. It has established a major field in condensed matter theory. ↑ up
Note 8 Aharonov-Casher effect
An effect in which the wave function of a particle moving in an electric field is multiplied by a complex exponential factor that depends on the magnetic moment of the particle. A similar effect is the Aharonov-Bohm effect, in which the phase part of the wavefunction of a charged particle changes in response to its motion in a magnetic field. ↑ up


