DATE2021.10.12 #Press Releases
Derive non-equilibrium thermodynamic laws that are universally valid in chemical reactions
Disclaimer: machine translated by DeepL which may contain errors.
Kohei Yoshimura (Department of Physics, 2nd Year Master's Student )
Sousuke Ito (Universal Biology Institute/ Lecturer, Department of Physics)
Key points of the presentation
- Discovery of two thermodynamic trade-off relations (Note 1), which are universally valid in chemical reactions.
- It was shown under general assumptions that the law, which was known only for stochastically behaving systems, also holds for deterministically (Note 2) changing chemical reaction systems.
- The paper demonstrates the universality of the thermodynamic trade-off relationship and provides new guidelines for the thermodynamic analysis of chemical reactions in nature, including metabolic and information transfer systems in living organisms.
Summary of Presentation
The thermodynamic properties of stochastically behaving non-equilibrium systems such as Brownian motion and molecular motors (Note 3) have been intensively studied in recent years. In the framework of what is called fluctuating thermodynamics, various thermodynamic laws have been discovered.
On the other hand, non-equilibrium systems are not limited to those that behave stochastically. For example, deterministic chemical reactions are important non-equilibrium phenomena that can be found in our daily lives, including in living organisms. However, in contrast to the development of fluctuating thermodynamics, the thermodynamic properties of non-equilibrium chemical reaction systems have been poorly understood.
Kohei Yoshimura, a graduate student, and Sousuke Ito, a Lecturer at the Graduate School of Science, The University of Tokyo, have discovered that by utilizing the intrinsic fluctuation index of chemical reactions, which had not been paid attention to before, the thermodynamic uncertainty relation and thermodynamic rate limit, which are thermodynamic trade-off relations obtained in the thermodynamics of fluctuations, are obtained even in deterministic chemical reactions. limit, which are the thermodynamic trade-off relations obtained in the thermodynamics of fluctuations.
The present study has revealed that these non-equilibrium thermodynamic laws are valid for essentially different systems, and supports the universality of the laws. The relationships proved in this study are expected to be used for thermodynamic analysis of individual and specific chemical reaction systems from a unified viewpoint, thereby deepening our understanding of biological processes that use chemical reactions.
The research results will be published in Physical Review Letters on October11 (local time). It has also been selected for an Editors' Suggestion.
Publication details
Most of the phenomena in the world are nonequilibrium phenomena. Therefore, the properties of non-equilibrium systems have long been studied since the framework of thermodynamics and statistical mechanics, which describe equilibrium states, was completed in the early 20th century. The thermodynamic properties of non-equilibrium systems with stochastic behavior, such as Brownian motion and molecular motors, have been gradually clarified over the past two decades through the development of a field called thermodynamics of fluctuation.
On the other hand, non-equilibrium systems are not limited to those that behave stochastically. A typical example is deterministic chemical reactions. Chemical reaction systems that are not in chemical equilibrium, in which a net reaction is in progress, or chemical reaction systems in which substances are exchanged with the outside, such as inside the bodies of living organisms, are examples of non-equilibrium chemical reaction systems. These phenomena behave deterministically if the system is large enough, so the theory of fluctuating thermodynamics cannot be used. The thermodynamic theory of deterministic chemical reactions has long been studied in a field called chemical thermodynamics, but it does not go far beyond the scope of equilibrium thermodynamics. Recently, non-equilibrium thermodynamic theory has been studied little by little, stimulated by the success of fluctuating thermodynamics, but it is still not very active. In particular, it has been little known whether the properties of nonequilibrium systems discovered in fluctuating thermodynamics also hold in chemical thermodynamics.
Graduate student Kohei Yoshimura and Lecturer Sousuke Ito of the Graduate School of Science, The University of Tokyo, have recently focused on the thermodynamic laws of non-equilibrium thermodynamics, especially the Thermodynamic Uncertainty Relation (TUR) and theThermodynamic Speed Limit (TSL), which have attracted much attention. We have proved that the two laws, TUR (Thermodynamic Uncertainty Relation) and TSL (Thermodynamic Speed Limit), which have attracted much attention recently, are also valid in the framework of chemical thermodynamics. TUR andTSL are explained below, respectively.
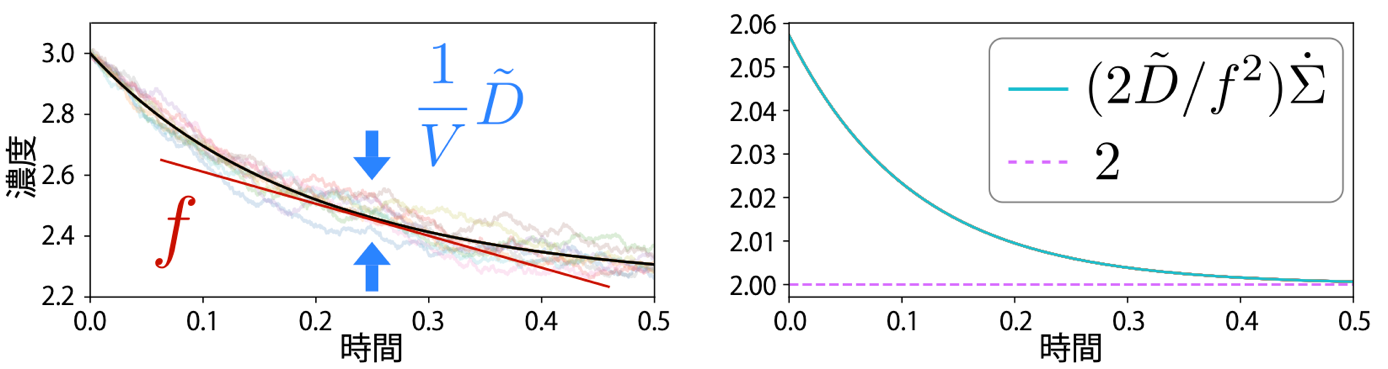
Figure: Schematic of the scaled diffusion coefficient and the thermodynamic uncertainty relationship in chemical reactions.
(Left) Time variation of concentration converges from stochastic behavior (light line) to deterministic behavior (black line) as the system grows. The magnitude of the decreasing fluctuation is proportional to the reciprocal of the volume, 1/V, from which the scaled diffusion coefficient is obtained. Although scaled diffusion coefficients are thus related to stochastic fluctuations, they can be defined using only physical quantities in deterministic dynamics.
(Right) The product of dissipation (entropy production rate) ∑ per unit time and the fluctuation represented by the magnitude D/ƒ 2 of the scaled diffusion coefficient D relative to the rate of concentration change ƒ cannot fall below a certain value (dotted line in the figure). In other words, these quantities cannot be as small as desired at the same time. In the figure, 2 is multiplied by 2 for historical reasons.
Next, we will discuss general velocity limits before explaining TSL. The rate limit is the lower bound on the time required for a system to change. Conversely, the time required to change from one state to another cannot be less than the speed limit when the speed limit exists. In the past few years, the existence of various rate limits in various physical systems, both quantum and classical, has been demonstrated and has attracted much attention. In particular, the rate limit using dissipation in nonequilibrium processes is called the thermodynamic rate limit (TSL), which generally expresses the fact that the smaller the dissipation, the longer the time required (or, more precisely, the longer the time required cannot be shortened). Although TSL was discovered in the thermodynamics of fluctuations, it should also have been obtained in deterministic dynamics, since dissipation itself has no direct relation to fluctuations. In this study, we again use scaled diffusion coefficients to prove that the TSL can also be obtained in deterministic chemical reactions.
The generality of these results is another feature of this study. Until now, most of the results concerning chemical reactions have been based on the assumption of the ideal nature of the system, which ignores intermolecular interactions, and the generality of the results has been unsatisfactory. The results of this study, which will not be discussed in detail here, are based on a generalized physical assumption called the local detailed balance relation, which is valid in general situations, including non-ideal systems. Also, our results are valid for deterministic chemical reactions, which are subject to nonlinear phenomena such as chemical oscillations (Note 4). In the paper, numerical experiments using the Lotka-Volterra equation confirm that the trade-off relation holds even in the case of chemical oscillations, and at the same time, the performance of the inequality is evaluated. As a result, it was confirmed that the inequality relation is useful even for systems that exhibit chemical oscillations.
This study shows that the non-equilibrium thermodynamic laws ( TUR and TSL ), which have been proved only for stochastic systems, are valid for essentially different systems such as deterministic chemical reactions, and proves that the laws are valid for a wide range of phenomena, that is, their universality.
The significance of the law is not only conceptual. In living organisms, chemical reactions are used in various processes such as metabolism, information transmission, and information processing. The trade-off relationship between yield, accuracy, and cost has been studied extensively for a long time, but these studies were conducted in specific or specialized chemical reaction systems. Therefore, it is hoped that the results of this study, which are based on a general framework, will provide a new perspective from which to consider chemical reactions in the body in a unified manner and help to deepen our comprehensive understanding.
This research was supported by the Grant-in-Aid for Scientific Research on Innovative Areas (Research Area Proposal Type) "Order and Design Principles of Life Revealed by Information Physics," by the Planning Research Group "Theoretical Study of Biological Information Processing by Information Thermodynamics" (Grant-in-Aid for Scientific Research ( 19H05796 )) and by the PRESTO "Theory of Biological Computing by Information Geometry and Thermodynamics" (JPJPJP) of the Strategic Basic Research Promotion Program. Computing Theory by Information Geometry and Thermodynamics" ( JPMJPR18M2), supported by the UTEC-UTokyo FSI Research Grant Program.
Journal
-
Journal name Physical Review Letters Title of paper Thermodynamic uncertainty relation and thermodynamic speed limit in deterministic chemical reaction networksAuthor(s) Kohei Yoshimura*, Sosuke ItoDOI Number 10.1103/PhysRevLett.127.160601 URL https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.127.160601
Terminology
Note 1 Trade-off relationship.
A relationship in which two quantities cannot be made efficient at the same time. Although sometimes used in everyday language, it is a topic of particular interest in nonequilibrium thermodynamics. The thermodynamic uncertainty relation proved in this study is a trade-off relation between fluctuation and dissipation, and the thermodynamic rate limit is a trade-off relation between speed and dissipation. In chemical reactions, various trade-off relationships have been known experimentally and theoretically, such as the trade-off relationship between efficiency (yield) and rate of production of ATP, a biomolecule known as the currency of energy in the cell ( T. Pfeiffer, et al., Science 2001 ). However, all of them were limited to the type of chemical reactions. ↑up
Note 2 Determinism and Probability Theory
In the time evolution of a system, if the initial conditions are the same, the subsequent changes in physical quantities are called deterministic, while those that are random and not one-way are called stochastic or probabilistic. If the experiment is conducted with a small number of molecules, the chemical reaction will be stochastic and the change in concentration will vary from trial to trial, but if the number of molecules is large, the change in concentration will be deterministic and constant each time. Even if the occurrence/non occurrence ofa chemical reaction is random, if the number of molecules is sufficiently large (e.g., if there are about 6✖️1023 Avogadro's numbers), the change in concentration will not be random. There may be many or few molecules involved in a chemical reaction in a living organism, but both are indispensable. ↑up
Note 3 Non-equilibriumsystems/phenomena
The state obtained by leaving the system for a sufficiently long time and waiting until there is no change is called an equilibrium state, whereas a state that is changing over time or a state in which there is no apparent change but heat or matter is exchanged with the outside world is called a nonequilibrium state. Phenomena in a non-equilibrium state are called non-equilibrium phenomena. For example, if a beaker is filled with chemicals and the lid is closed, the system will eventually reach equilibrium. On the other hand, if a net chemical reaction is in progress before equilibrium is reached, or if substances are supplied and collected from outside, the system is a nonequilibrium system in a non-equilibrium state. Thermodynamics describes universal properties that equilibrium systems possess, and there have long been attempts to construct such a theory for non-equilibrium systems and non-equilibrium phenomena. ↑up
Note 4 Chemical oscillations, nonlinear phenomena
Nonlinear phenomena are phenomena caused by the nonlinearity of interactions and include chaos, turbulence, and chemical oscillations. Chemical oscillation is a phenomenon in which the concentration changes periodically as a chemical reaction proceeds, the most famous example being the Belousov-Zhabotinsky reaction ( BZreaction ), which was first discovered. You can find many videos by searching for "BZ reaction" on video websites. There are many models that show chemical oscillations, but in this study, the Lotka-Volterra equation (a differential equation with a solution that oscillates in time, originally representing changes in predator and prey populations) was used as a model for chemical reactions to confirm the results. ↑


