DATE2021.03.13 #Press Releases
Solving a 30-year-old conundrum in quantum many-body systems:
Fundamental properties of the SU(N) Hubbard model revealed
Disclaimer: machine translated by DeepL which may contain errors.
Hironobu Yoshida (Department of Physics, 1st Year Master's Course)
Hosho Katsura (Associate Professor, Department of Physics / Trans-scale Quantum Science
(International Collaborative Research Organizations/ Institute for Physics of Intelligence)
Key points of the presentation
- We have discovered a new method to analyze the properties of the SU(N) Hubbard model (Note 1), which has long been considered difficult to treat theoretically because conventional methods cannot be applied.
- For a wide class of SU(N) attractive Hubbard models, we have rigorously clarified the fundamental properties of their ground states (Note 2), such as the number of particles and long-range order.
- This study opens up new directions for the analysis of quantum many-body systems and is expected to lead to further developments in this field.
Summary of presentation
Atoms and molecules are the basic elements that make up the materials around us. Microscopic atoms and molecules are known to obey quantum mechanics, and their fundamental laws are well understood through studies accumulated in the past. However, in matter, many microscopic constituents come together and interact with each other. Understanding their collective behavior from the viewpoint of quantum mechanics is a very difficult problem, which is called the quantum many-body problem. One of the quantum many-body problems is the SU(N)-attractive Hubbard model, a physical system in which particles with multiple degrees of freedom are strongly attracted to each other (Fig. 1). This system has recently been realized by atoms trapped by lasers and has attracted much attention.
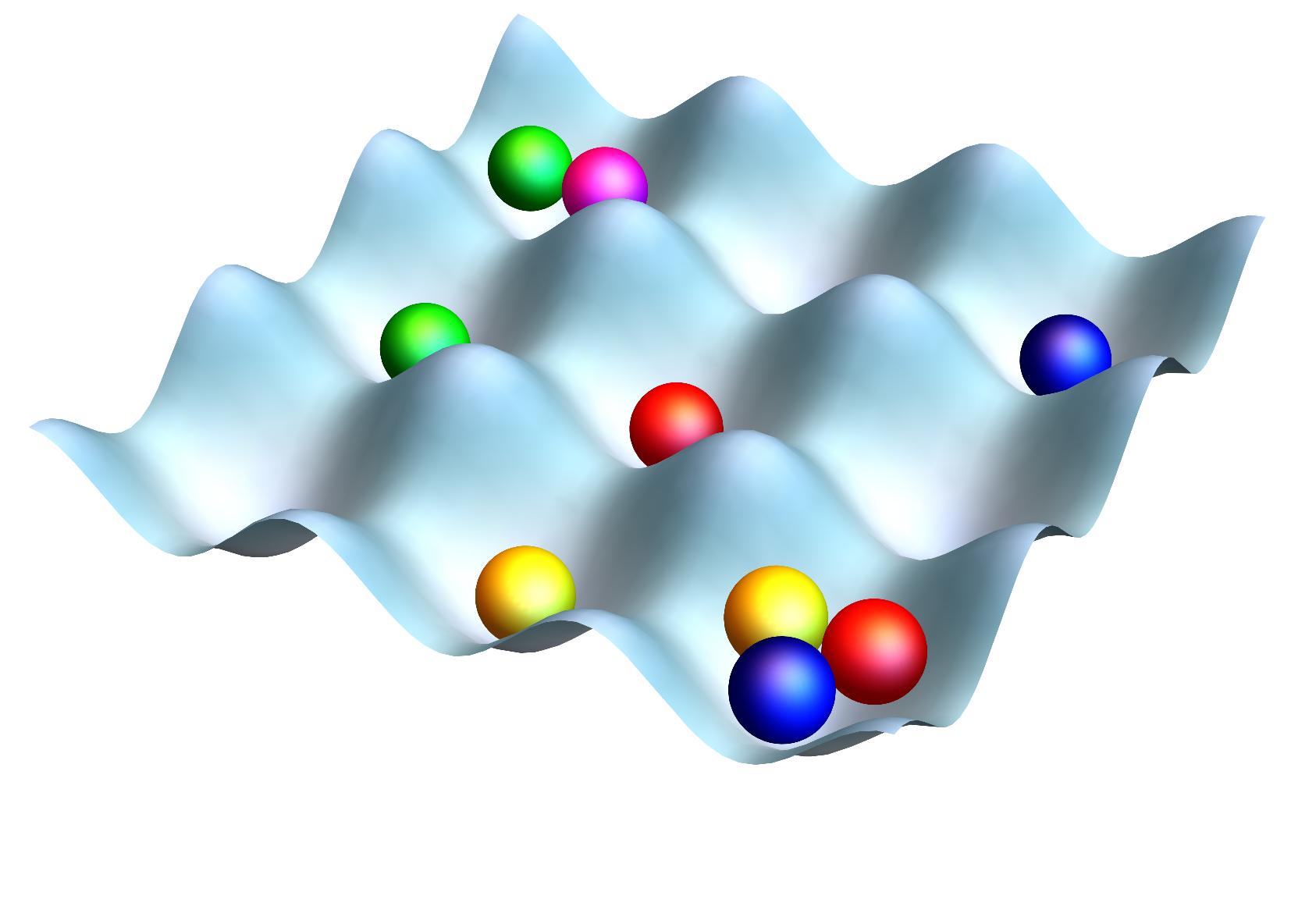
Figure 1: Conceptual diagram of the SU(N) attraction Hubbard model. Particles with multiple colored degrees of freedom are in motion as they jump between valleys (sites). Experimentally, the particles are atoms, and the mountains and valleys are realized by laser waves.
Hironobu Yoshida, a graduate student and Associate Professor Hosho Katsura, a master's student at the Graduate School of Science, The University of Tokyo, have rigorously clarified the fundamental properties of the ground state of a broad class of SU(N) attractive Hubbard models using the mathematical structure of the Mayorana particle (Note 3 ). Conventional methods proposed some 30 years ago were not applicable to this system, and the theoretical treatment of the system has been considered difficult.
This study not only deepened our understanding of the SU(N) Hubbard model of attraction, but also opened a new direction for the analysis of quantum many-body systems. Further development of this field is expected in the future.
This research result was published in Physical Review Letters on March 12. It was also selected as Editors' Suggestion .
Publication details
Research Background
The SU(N)-attracting Hubbard model is a physical system in which particles with multiple colored degrees of freedom are strongly attracted to each other. The Hubbard model was originally introduced to describe the motion of electrons in solids and is still being studied intensively. The electron has the property of being a small magnet, called spin, and has two degrees of freedom, upward and downward. Let us assume that these degrees of freedom are "color" degrees of freedom. The case with N=2 degrees of freedom of this color corresponds to the original Hubbard model, and when this is increased to N ( = 3,4,5,...) colors and there is an attractive interaction between the particles, this is the SU(N) attractive Hubbard model. This model has attracted much attention in recent years, as it has been experimentally realized by atoms trapped in lasers. The color degrees of freedom correspond to the nuclear spin degrees of freedom of the atoms in the experiment. As shown in Figure 2, in this model the N-color particles follow the following three rules of motion.
(1) Particles exist on a lattice and move by jumping between points (sites) on the lattice.
(2) No more than two particles of the same color can exist at the same site (Pauli's exclusion rule).
(3) When multiple particles (with different colors) come to the same site, their energy is lowered due to gravitational attraction.
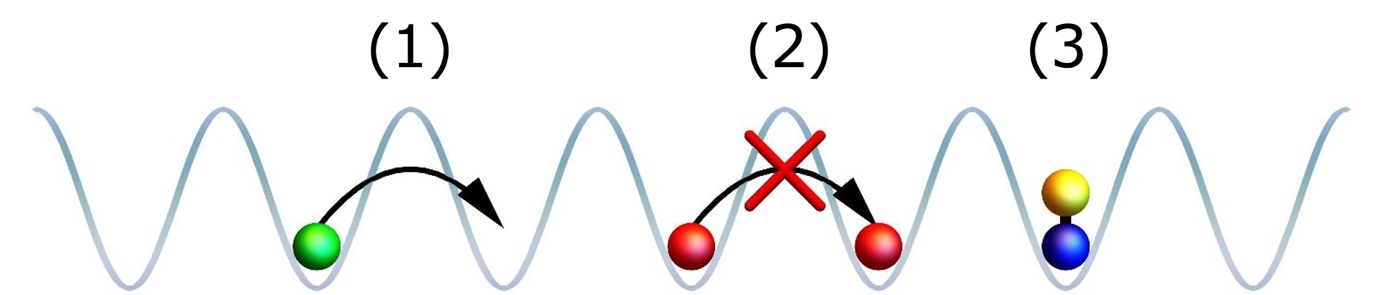
Figure 2: Rules for particle motion in the SU(N) attraction Hubbard model.
Although this physical system appears simple at first glance, it has been very difficult to analyze. One reason is that the possible configurations of the particles explode as the number of sites and particles increases (Figure 3).

Figure 3: All possible arrangements with three sites and one particle of each of thethree colors. The number of possible placements explodes as the number of sites and particles is increased, making it very difficult to handle.
Therefore, it is not practical to solve this model directly, even with very powerful computers. Therefore, various approaches have been taken to analyze it without solving it directly, one of the most powerful of which is the mathematical method of spin mirror positivity. This method, published by Elliott Leape (see note 4) in 1989, is a very powerful method for rigorously investigating the ground-state properties of the original SU(2) Hubbard model. However, since this spin mirror positivity method uses upward and downward spin symmetry, it could not be applied to cases where the color degrees of freedom are larger than 2.
Details of Research
The research group has applied the mathematical method of Majorana mirror positivity, recently discovered by Arthur Jaffee (Note 5) and others, to rigorously show the fundamental properties of the ground state of a wide class of SU(N)-attractive Hubbard models. In the following, we describe this mathematical method. Particles satisfying rule (2) described in the research background are called Fermi particles. The Fermi particle can be decomposed into two Majorana particles. Mayorana mirror positivity is a method that uses the symmetry between these two Mayorana particles and can be applied to cases with more than two degrees of freedom. Using this method, we can show an inequality with respect to the energies of the possible states of the system. Since this inequality is independent of the number of sites, it can be used to analyze systems with a large number of sites and particles.
Using this method, the group has shown that the ground state of the SU(N) Hubbard model of attraction on the bipartite lattice (Note 6) is invariant with respect to the number of ground states (degeneracy), the number of particles, and transformations that swap the color degrees of freedom. We also showed that when the number of sites on the two sublattices (Note 7) differ macroscopically, as in Figure 4, the system exhibits charge density wave (Note 8) like ordering.
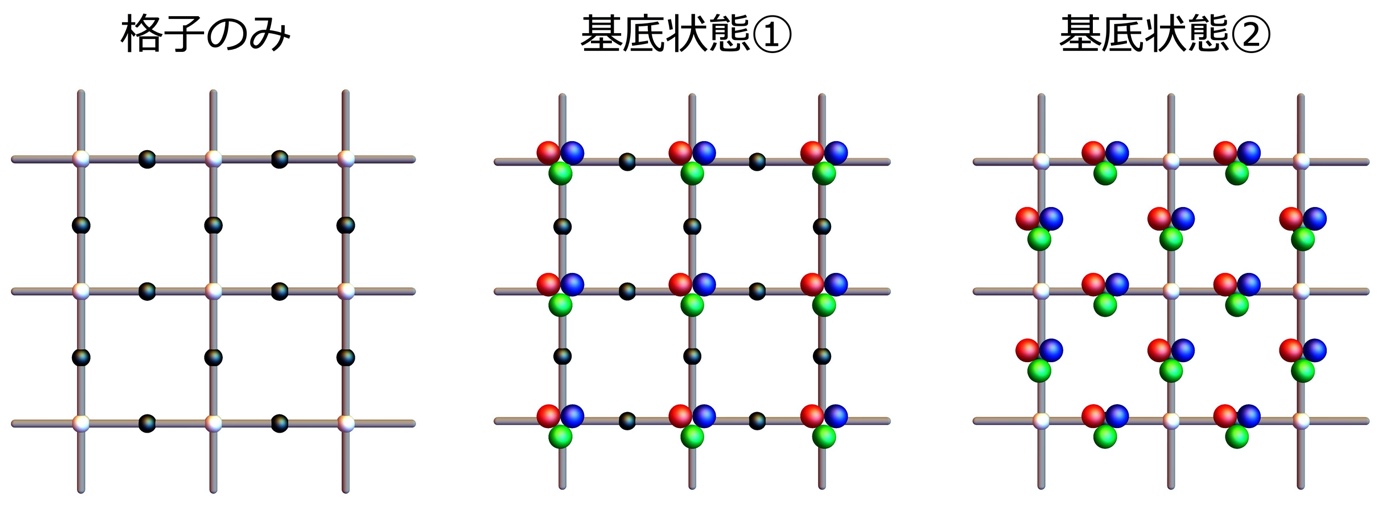
Figure 4: (left) Lattice consisting of black and white sites. The number of black sites is twice the number of white sites. The collection of black sites and the collection of white sites are each a sublattice. (center, right) The ground state for N=3, when the attractive interaction is very large. There are two ground states, as shown in the center and left figures. In the center figure, particles are localized at the white sites, and in the right figure, particles are localized at the black sites, creating shading in the density of particles (charge density waves). In this study, we have shown that the ground state is the state in which shading is created in the density of particles, regardless of the strength of the gravitational interaction.
Future Prospects
The SU(N) Hubbard model, which has been studied since its realization by laser-trapped atoms, has attracted much attention because of its potential to exhibit new quantum states. This study provides a new direction for research on this physical system and is expected to promote further development of research in this field. Future directions include extensions to physical systems with symmetries different from those analyzed in this study. We would also like to investigate in which cases the methods of this study can be used in general.
Journal of Publication
-
Journal name Physical Review Letters Title of paper Rigorous Results on the Ground State of the Attractive SU(N) Hubbard ModelAuthors Hironobu Yoshida* and Hosho KatsuraDOI Number 10.1103/PhysRevLett.126.100201 URL
Terminology
1 SU(N)Hubbard model
A model of a quantum system in which particles with N degrees of freedom interact; when N is 2, the model describes the motion of electrons in a solid; when N is larger than 3, the model is realized by atoms trapped by lasers and has attracted much attention in recent years. ↑ up
Note 2 Ground state
The lowest energy state of a quantum system. ↑ up
Note 3 Mayorana particle
A particle theoretically proposed by Italian physicist Ettore Majorana in 1937. It has the property that the particle and the antiparticle are the same, and has attracted attention in the context of spin liquids and quantum computation. ↑ up
Note 4 Elliott H. Lieb (1932~)
American mathematical physicist. Numerous very distinguished achievements in the fields of statistical mechanics, condensed matter theory, and functional analysis. ↑ up
Note 5: Arthur Jaffe (1937~)
American mathematical physicist. He is best known for his work in constructive field theory and as the first Director of the Clay Mathematics Institute, famous for the Millennium Sweepstakes. ↑ up
Note 6 Bipartite lattice
A lattice such that when the sites on the lattice are painted in two different colors, all two adjacent sites can be painted in different colors. For example, a lattice consisting of squares laid out on a plane is a bipartite lattice, but a lattice consisting of equilateral triangles is not. ↑ up
Note 7 Partial lattice
When a bipartite lattice is painted in two colors, it is a collection of sites painted in each color; a bipartite lattice consists of two sublattices. ↑ up
Note 8 Charge density wave
A state in which periodic shading is created in the density of particles. ↑


