DATE2022.02.10 #Press Releases
Why were the bumps in the first universe created symmetrically?
Disclaimer: machine translated by DeepL which may contain errors.
Jason Christiano, First Year Ph.D. Student, Department of Physics
Junichi Yokoyama, Professor, Research Center for the Early Universe
Key points of the presentation
- Inflation in the Early Universe (Note 1 ) Theoretically showed that the density bumps created during expansion must be symmetric with the same amount of convex and concave parts with high precision.
- Density Fluctuation (Note 2) We analyzed the formation of density fluctuations based on quantum field theory and found that unless the distribution of convexities and concavities is symmetric with high precision, the amplitude of the fluctuations deviates significantly from the observation.
- This result provides a clue to identify the origin of inflation.
Summary of Presentation
While our universe is globally uniformly isotropic, there exist structures of various scales such as stars, galaxies, and galaxy clusters. This is explained by the idea that a large uniformly isotropic space was realized by a rapid expansion called inflation, which occurred immediately after the birth of the universe, and that convexities and concavities, which became the seeds of structures, were generated based on quantum fluctuations in the vacuum of the elementary particle field (Note 3) that caused the inflation. The bumps, which are only 1/100,000 of a millionth of a degree, have been observed as temperature fluctuations in the cosmic microwave background radiation (Note 4), which represents a trace of this process. Due to the symmetry of the vacuum, quantum fluctuations produce the same amount of both convexity and concavity, so if we can observe the discrepancy between the two, we can measure the interaction of the inflated fields, which cannot be revealed by ground-based accelerator experiments. Applying quantum field theory to cosmology, Jason Christiano, a graduate student in the Department of Physics at the Graduate School of Science, The University of Tokyo, and Professor Junichi Yokoyama of the Research Center for the Early Universe, have shown that these interaction terms not only produce a discrepancy in the distribution numbers of both convex and concave, but also shift the theoretical values of the amplitudes of the convex and concave by In order for the theory to reproduce observations, the distribution of the convexo-concave must be symmetric, and the field interaction of the inflated subatomic particles must be less than about one-tenthof the limit obtained by current observations. The results of this study are as follows.
Presentation
When we look at the night sky with the naked eye, we see many stars, and when we look through a telescope, we observe many galaxies and galaxy clusters. On the other hand, when we look at the universe as a whole, we see a vast expanse of uniform space extending over tens of billions of light years. This property of the universe is explained by the fact that the universe underwent an explosive and rapid expansion called inflation prior to the Big Bang (Note 5).
While inflation greatly expands the universe to achieve uniform space, it occurs when the universe was much smaller than a hydrogen atom, so quantum effects at work in the microscopic world play an important role.
Inflation of the universe is thought to be caused by the energy of some field called the "infraton (Note 6 )" that uniformly fills space. The ultimate goal of research on inflationary cosmology is to clarify the nature of this field in the context of particle physics. The universe would have been essentially in a vacuum because all other matter would have been completely diluted by the rapid expansion of the universe during inflation. If we develop the quantum theory of the inflaton in such a rapidly expanding universe, we find that as the universe expands, the inflaton's convexities and concavoconcavoconcavoconcavoconcavoconcavoconcavoconcavoconcave one after another. As a property of fluctuations around the vacuum, convex and concave regions of various heights (amplitudes) always appear with the same frequency, and their distribution follows a normal distribution (Gaussian distribution). The normal distribution is also the distribution used to calculate deviation values in mock examinations, where areas higher and lower than the mean appear with the same frequency, maintaining a uniform vacuum as the mean. However, some of the inflaton's convexities and concavities change as a result of interactions, either breaking up or merging, resulting in a discrepancy between the frequencies of convex and concave regions. The degree of this discrepancy is determined by the strength of the interaction of the inflaton as an elementary particle, so if we can observe the number and height (amplitude) of the concavities and convexities, we can gain significant insight into high-energy particle physics that cannot be obtained from accelerator experiments. (Figure 1).
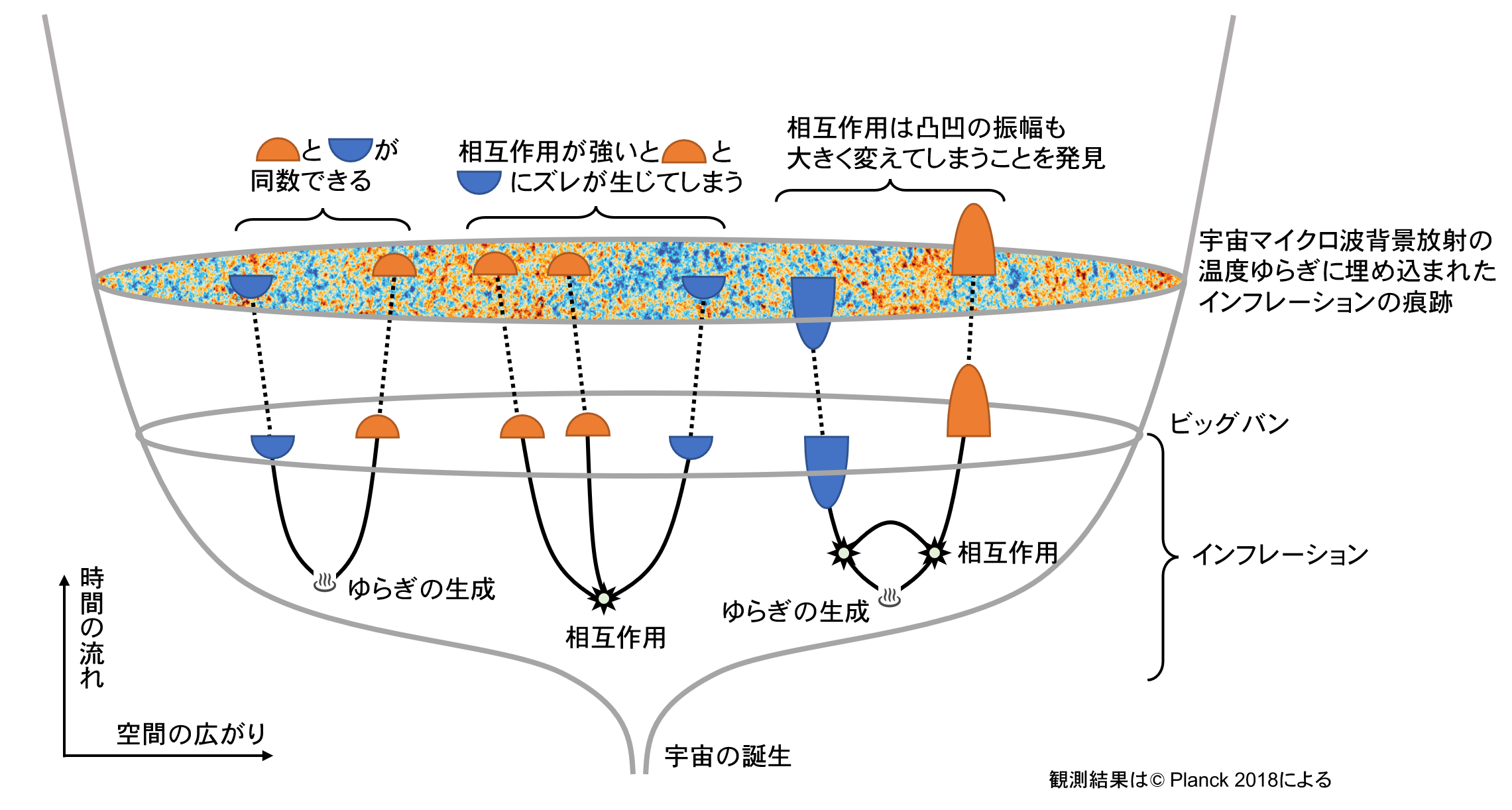
Figure 1: Conceptual diagram of density fluctuation production, which is the seed of galaxies and galaxy clusters in the inflationary universe. Quantum fluctuations produce an equal number of convex and concave regions, but strong inflaton interactions cause a misalignment between the two. However, it has now been discovered that these interactions also significantly change the amplitude of density fluctuations, imposing a limit on the strength of the interactions that is 10 times stronger than before.
The bumps created in this way are then stretched by subsequent inflation, so that the universe is eventually filled with bumps of various sizes. The bumps are only about 1/100,000th of the average energy, so the fluctuations are very slight, about the size of a 1 mm high ripple in an ocean 100 meters deep. Even such a slight convexity and concavity has a stronger gravity in the densely convex region than in the concave region, which attracts more and more matter around it, eventually developing into cosmic structures such as stars and galaxies.
Traces of these small bumps created during inflation can be observed by measuring the temperature of the cosmic microwave background radiation. Planck satellite all-sky observations have revealed that larger bumps formed earlier in the inflationary process have slightly larger amplitudes than smaller bumps. They also find that the frequency distribution of the bumps of different amplitudes is perfectly consistent with a normal (Gaussian) distribution to the best of the current observable precision. In other words, the interactions of elementary particles that represent the collective discretization of the inflaton's convexo-concave have only small values below the limit of measurement.
Jason Christiano, a graduate student, and Professor Junichi Yokoyama of the Graduate School of Science at The University of Tokyo have analyzed how these inflaton interactions affect the amplitude of the convex hull itself by applying the quantum field theory usually used to study particle theory to cosmology. In previous studies, it was thought that even if the inflaton interaction caused a set discretization of the convexo-concavity, the effect of such an interaction would be completely negligible, since it would only add another 1/100,000th of a correction to the quantity considered at the one point where it occurred. In fact, theoretical calculations that did not take this into account reproduced the observed data very well. On the other hand, previous studies that attempted to calculate such corrections assumed that the same number of bumps of any size could be made, resulting in only physically meaningless infinite quantities, as is often the case in quantum field theory calculations. The researchers succeeded in getting this value correct by performing a calculation that correctly incorporated even the size distribution of the convexo-concavities. They found that even if these corrections are negligible at a single point, they must add up over the entire exponentially large inflationary universe, and unless the inflaton interactions are sufficiently weak, they result in corrections well in excess of 1 part in 100,000, and the theoretical calculations that ignore these corrections, which were used previously We found that the theoretical calculations that ignored this correction used in the past would break down. This result means that for theoretical calculations of inflation to be consistent with observations, the inflaton interaction must be even less than about one-tenth of the current observational limit, and deviations from the normal distribution of convexo-concave distributions will not be detectable in the future (Figure 2).
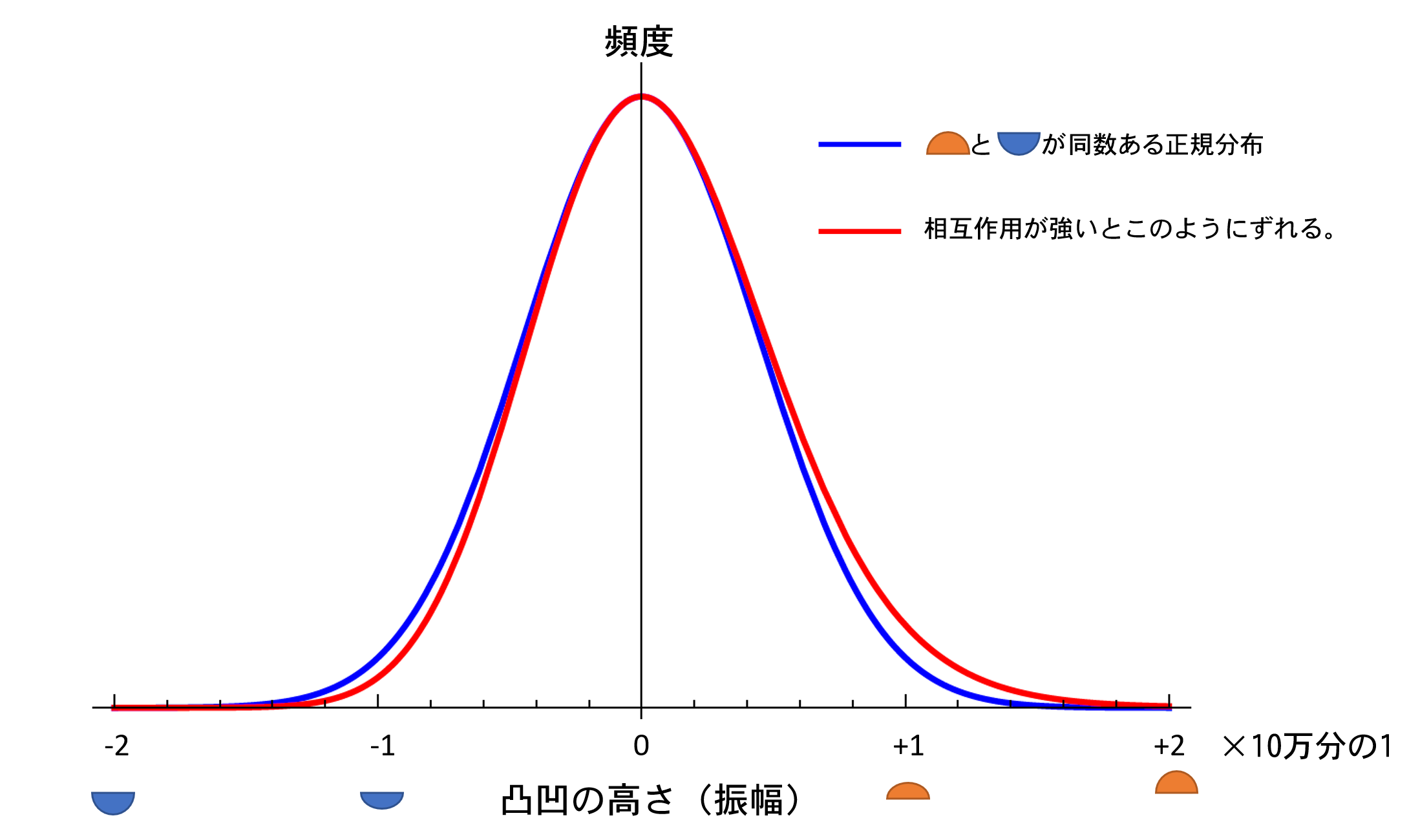
Figure 2: The distribution of the magnitude of quantum fluctuations in the vacuum follows a symmetric normal distribution around the mean (Gaussian distribution), as depicted by the blue line, but becomes asymmetric as the red line when the effect of the inflaton interaction is taken into account. The present study shows that the strength of the interaction must be less than1/200th of that of the red line in the figure. Such a distribution is indistinguishable from the blue line.
This also provides a clue to the particle physics theory describing inflation.
Journal of Publication
-
Journal name Physical Review LettersTitle of paper Why Must Primordial Non-Gaussianity Be Very Small ?Authors Jason Kristiano and Jun'ichi YokoyamaDOI number https://doi.org/10.1103/PhysRevLett.128.061301
Terminology
1 Inflation
A rapid cosmic expansion that occurred immediately after the creation of the universe. It is believed that the universe underwent a maze-like expansion in a much shorter time than one thousand trillionth of a trillionth of a trillionth of a trillionth of a trillionth of a trillionth of a trillionth of a second, and became 30 orders of magnitude larger in a fraction of a second. ↑up
Note 2 Fluctuation
In the microscopic world of the early universe, all matter has the properties of fine waves, according to quantum theory. Since waves are never stationary, all physical quantities always deviate slightly from their average values when viewed in detail and fluctuate. This deviation is called fluctuation. ↑up
Note 3 Field of elementary particles
First, a field is a quantity that has some value at each point in space. A familiar example is the magnetic field described by magnetic lines of force around a magnet. The magnetic field represents the strength and direction of the magnetic force at each point. All elementary particles are described by a field (ba) that represents their properties and distribution. ↑up
Note 4 Cosmic microwave background radiation
In the hot, dense early universe, electrons and protons exist in discrete ionized states, and light is scattered by electrons and cannot fly straight. As the temperature of the universe decreases, the electrons are captured by the protons and become hydrogen atoms, and light can fly straight without being scattered. The farthest light we can observe is the last light scattered by the electrons at this time, which is what we observe today as cosmic microwave background radiation. Just as we can observe the light coming from the surface of a cloud on a cloudy day and know the shape of the cloud, we can tell what kind of density fluctuations the universe had at that time by observing the cosmic microwave background radiation. ↑up
Note 5 Big Bang
Traditionally, the term "Big Bang" refers to the great explosion that occurred at the creation of the universe, but today it has a different meaning because the universe is thought to have begun through inflation. Inflation dilutes all the matter and radiation, if any, that existed before, so thermal radiation must be created from the energy of the infraton (Note 6) after inflation ends. This process is called the Big Bang today. ↑up
Note 6 Infraton.
Inflation of the universe is caused by matter such that its energy density remains constant even as the universe expands. Unknown matter with such properties is called infraton. Infratons are thought to be some kind of elementary particle field (Note2 ) that follows the quantum theory of ( Note 3). ↑up


