純粋数学者は「エルゴード群論」で世界の深淵を目指す

純粋数学者は「深淵」を目指す……。それが、我々一般人にとっての数学者のイメージだ。このイメージによってさまざまな先入観が生まれる。深淵を目指すくらいだから、きっと天才であるに違いない。天才だろうから、きっと変人も多いに違いない。数学という閉じられた世界の住人なのだから、きっと芸術家のように孤高であるに違いない。きっと、きっと、きっと……。

実際、一般人である我々が知っている歴史上の高明な数学者を思い浮かべてみると、それが正しく思えなくもない。古代ギリシャのピタゴラスから始まって、フィボナッチ、デカルト、フェルマー、パスカル、ニュートン、ライプニッツ、オイラー、ガウス、リーマン、ポアンカレ、ノイマン、チューリング、シャノン。日本人なら関孝和、高木貞治、岡潔、谷山豊。そしてもっとも最近では望月新一。いずれも傑出した才能の持ち主で、その中には強烈な個性の人も含まれている。また、天才芸術家のイメージに近い孤高さを持ち合わせている人もいる（特に岡潔など）。さてさて、この数学者像は偏見なのか真実なのか。

東京大学の数理科学研究科にも、我々に「天才っぽいな」と思わせる若き数学者がいる。木田良才教授。京都大学3回生の時に「飛び級」をして大学院へ。博士課程時代に書いた論文が大きく注目され、数学界にその名を轟かせた。博士号取得後は独・マックスプランク研究所、東北大学、京都大学を経て、東大で30代にして教授となった。柔和なその笑顔からは、苛烈な個性の天才というよりも、温厚で真摯な研究者という印象を与える。さて、彼はどんな深淵を覗き込んでいるのだろう。

自分の研究テーマをエルゴード群論と命名

木田教授が研究しているのは「群論」である。我々のような数学素人には「いくつかの性質（ひとつの演算ができる、結合法則が成り立つ、単位元がある、逆元がある）を持っている『数の集まり（group：グループ）』を群と呼ぶ」というきわめてふんわりしたことしか分からない。

「そうそう。定義としては、『群』とはそのような代数的なものです。だけど、幾何の視点も入ります。よく『群って何のためにあるんですか』と聞かれるのですが、たとえば、群は『図形のきれいさを表す指標』と考えることができます。『きれい』というのは人によって印象がちがうとは思うんですが、たとえば、円、三角形、四角形と3つの図形を見比べると円が一番きれいですよね。角がないし。そのような『きれいさ』を表せるのが群という概念です」

正三角形を回転して重ねられるのは3回。120度ずつ回して3回重なる。正方形なら90度ずつ回して4回重ねられる。この「重ねられる回数」が多いほど、きれいということになる。円はどれだけ回してもすべて重なる。だから、一番きれいだということになるわけだ。そのような重ねる操作の集合も群なのだそうだ。

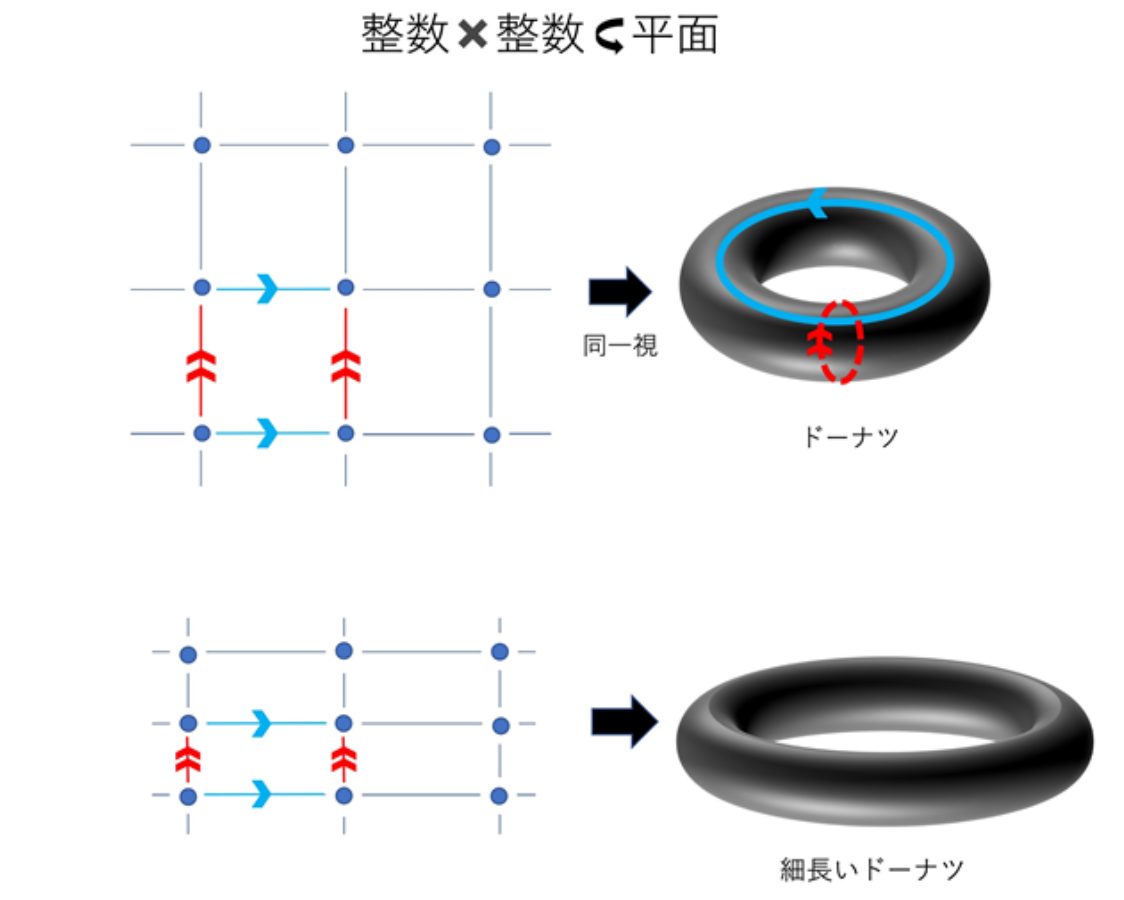
「いろいろな数学の問題は、群の言葉で定式化することができます。群に置き換えることで元々の問題がよく分かるのです。だから、群は数学全体の中で基本言語的な役割を果たしている概念です。たとえば……平面の中に『整数の点』がてんてんてんてんとありますね。これをこのように正方形が連なっているように考えると、縦に1個ずらしたり横に1個ずらしたりすると、こことここは同一視される。それを続けて同一視してつなげていくとドーナツの形になる。そのように、ドーナツの幾何の問題は『整数 × 整数の平面への群の埋め込み方』というものに置き換えられるわけです」

つまり、群はいろいろな数学のツールのようにして使う。ほとんど、どの分野でも出てくるものらしい。それで、木田教授の研究テーマはその群とどのような関連があるのだろう。

「ぼくの研究テーマは『離散的な群』です。今の話の整数 × 整数以外にも、もっと飛び飛びの離散的な群ってたくさんあるんですよ。いろいろな数学で出てくる。『ある２つの離散的な群が連続的な群に格子状に埋め込めるかどうか』ということを考え、埋め込めたら『その２つの離散的な群は同じである』と言うことにします。ぼくの研究は、そのようにして離散的な群を分類していこうという研究です」

群とドーナツの幾何学

そういえば、WEBで木田教授の文章を探していたら、「ぼくは自分の研究テーマを『エルゴード群論』と呼ぶことにしました」という記述を見つけた。

「ああ、そうです。自分の研究テーマを『エルゴード群論』と呼んでいます。元々の定義からすると群は代数的なものですが、1990年代にミハイル・グロモフという数学者が群論に幾何学的な視点を導入して『幾何学的群論』という分野を作りました。ぼくの研究テーマはその幾何学的群論の兄弟みたいな分野です。英語では『measured group theory』という名前がついていますが、『測度付き群論』という直訳がどうもネーミングとしてかっこ悪いなと思って、『エルゴード群論』と呼ぶことにしました。エルゴード理論を用いて離散群全体の世界をどのように捉えるべきかを追求する分野なので、エルゴード群論です。エルゴード理論とは『測度がある空間への群の作用を扱う分野』です。そういう『測度を持った空間への作用』を用いて離散群を研究しているのです」

幾何学的群論、測度、エルゴード理論など、WEBで検索するとたくさんの解説が出てくる。興味のある読者はいろいろと調べてみてほしい。

辛い研究生活の後に突然、アイデアが降臨

さて、木田教授は「純粋数学」の研究者である。数学は純粋数学と応用数学に大別される。純粋数学は文字通り、純粋な数学で、いわば数学そのものの理論を拓いていく分野だ。数式によって抽象的な思考を深めていく。一方、応用数学は、数学を世界のあらゆる事象に応用していく分野。自然現象を数学により記述することから始まって、社会のさまざまなことまでも数学で記述していく。

20年以上前から、金融派生商品であるデリバティヴの取引には高等数学が使われていたし、気象のシミュレーションや最近流行りのデータサイエンスでも数学が鍵となる（数学＋計算科学という形が多い）。一般人から見ると、応用数学は具体的な事象が関わってくるので、理解できないとしてもイメージしやすい。しかし、純粋数学はどこまでも抽象化された世界に見える。純粋数学者は、数式以前に頭の中でイメージしているものがあるのだろうか。

「最初から抽象的なことをやっているという意識はないんです。さきほど話したような整数を平面に埋め込むといった『絵に描けるような具体的なイメージ』から始まって考えていきます。でも、論文にする時には本質的な答えに至るための必要最小限な記述から始めるので、抽象的なことだけに見えるのかもしれません」

天才っぽいと思っていた木田教授がいきなり身近に思えてきた。現実的な話に入っていこう。木田教授は高校生ぐらいの頃から数学者になろうと思っていたのだろうか。

「全然、思っていませんでした（笑）。高校生の時は数学と物理が好きで問題を解くのが好きでした。けっこう難しい問題が解けたら、それでうれしいというかんじ。『将来、これを突き詰めたい』みたいな思いはなくて。大学生になってからも、やっぱり単に『好きだ』というかんじでやっていました。大学生になって、数学の本を眺めていると高校の頃にやっていた数学と雰囲気が全然違うんですよ。よく図書室で数学の本を眺めていて『いろいろな数学があるんだな』と楽しんでいました。ところが、大学院生になったら、それが一転したんです」

大学院生になった木田青年は数学をやるのがいきなり辛くなった。好きで問題を解いたり本を眺めたりしているだけでなく、「研究」をしなければならなくなったからである。

「今までは問題を解いていれば良かったけれど、大学院生になったら論文を書かなきゃいけないので、そのためのテーマを見つけなければならない。つまり、自分で問題を作らなければならないわけです。『こういう論文を読んでみたら』と指導教員も勧めてくれたりしたのですが、読んでも自分で論文を書くことにはなかなか繋がらなくて。本当に苦行っぽいかんじでした。修士課程1年くらいの頃はまだ心の余裕があったんですけど（笑）、2年になると『なんか、全然できない』というかんじになっていきました。とにかく真似するしかないなと思って真似できそうな論文を漁って『これをちょっと変えたらできるかな』みたいなことばかり考えていました。それでも、なんとか修士論文は書き終え、その後、博士論文も書くことができました。それで……書き終えてほっとしている時期にイワノフのサーベイを読んでいて、『あ！』と気づいたんですね。まさに雷が落ちるようなかんじでした！」

これぞ天啓とでも言うべきか。ものすごいアイデアが木田青年のもとに降ってきたのである。

「かなり興奮した記憶があります。いきなりの『ひらめき』って、今までの数学人生でその時だけかもしれません。もう一生ないかもしれないし。結局、マックス・プランク滞在の前半はそのアイデアをちゃんとした形にするという作業に使いました。幸い、そのアイデアを基にした論文は数学界の著名な先生らから非常に良い評価をいただくことができました」

純粋数学者もちゃんと世界と繋がっている

一瞬のひらめきをきっかけに書き上げた論文。その時が数学者になろうと思った時期だったのだろうか。

「数学者になろうと思ったのは博士課程を修了してドイツのマックス・プランク研究所に行ってからです。マックス・プランク滞在は1年間だったのですが、公募に応募する時も『もし、落ちたら、数学者以外の別の道を探そう』と思っていました。その後、東北大学が助教として採用してくれたので、その時から数学者になったかんじですね」

経歴から勝手に「天才っぽい」と思っていたが、数学者になるまでには大いなる苦悩や葛藤があったのだ。だから、研究者として採用されてから、初めて数学者としてやっていく覚悟を持ったということなのだろう。

「辛かった修士の時期があったので『挫折がなかった』という感覚はまったくありません。実際、数学の研究が苦行であることは今も続いていますよ。教員としての他の仕事も増えますし、家庭もあるので。家で食事を作ったり（笑）。研究に集中するには体力も必要だし。やっぱり、あの時は体力も時間もあったという最高の状況でアイデアが降ってきたということですね」

スポーツ選手が金メダルを取り続けるのが大変であるのと同様、数学者として目覚ましい結果を出し続けることは本当に大変なことなのだろう。一人で奮闘して結果を出していく純粋数学者。一般人が「孤高」のイメージを抱くのも自然なことだ。純粋数学者である木田教授は、多くの応用数学者の姿を見ていてどのように感じているのだろうか。

「自分の数学が社会に応用できて人々に喜んでもらえる応用数学者は素直に『うらやましいな』と思います。さきほど話したエルゴード群論を専門にしている日本人数学者って、ぼく一人なんですよ、実は（笑）。だから、良い言い方をするなら『オリジナリティが高い』ということになるのでしょうけれども、悪い言い方をすれば『とても狭い世界でやっている』ということですよね。近い分野の方に自分の成果を話しても理解してもらえなかったり、苦労を分かってもらえなかったりということもあります。しかし、自分としては孤立、独立しているとは思っていません。純粋数学だからといって抽象化ばかりしていると、行き詰まることもあります。そういう時は別のテーマを探すわけですが、たとえば、自然からヒントやモチベーションを得て新たなテーマに行き着くことも多い。つまり、純粋数学者もちゃんと世界と繋がっているんです」

世界と繋がる純粋数学者。それだけで一編の小説になりそうな物語性を感じるではないか。

多様な数学的価値観を身につけよ

短い時間ではあるけれど、ここまで話を聴いてきただけで、やはり、世界の理性を一身に背負っているような純粋数学者は魅力的だ。世の中の高校生、受験生、学部生の中に「数学者になりたい」と思う人が多数いるのもうなずける。そんな「数学者になりたい若者」に対して、何かメッセージをいただこう。

「うーん、一言で言うならば、『多様な数学的価値観を身につけよ』ということかな。高校生が知っている数学と比べると、数学の世界ってすごく広くて深くて多様なのです。だから、大学の数学などに触れて、いろいろな数学を知って、数学的な価値観を広げてほしい。後々、自分で問題設定することにも影響してきます。それから、価値観は人によってそれぞれ違うので、友達と数学のことを話してみてほしい。高校生や受験生なら数学好きの友達と、数学科の学部生だったらクラスの人と数学のことを話してみてください。今までよく知っていた簡単な数学的事実でも『ああ、そこまで深く考える人もいるんだな』と気づかされたりします」

多様な数学的価値観……。哲学者が世界の深淵に近づいていくように、数学者も自らの価値観に立脚して世界の深淵を目指していく。さて、その先には何があるのか。

貴方が数学者になった時、きっとその先を目撃できるに違いない。

※2022年取材時
文／清水修（ACADEMIC GROOVE）
写真／貝塚純一