Pure mathematicians approach the abyss. That’s the layperson’s typical view of mathematicians, an image that gives rise to various preconceptions:
They must be geniuses because they approach the abyss. If they’re geniuses, they must include a lot of eccentric types. As inhabitants of the closed world of mathematics, they must have a solitary nature like artists. They must, they must, they must….
In fact, if you think of the eminent mathematicians of history that are familiar to laypeople, this image just doesn’t ring true. Starting from Pythagoras in ancient Greece, we think of Fibonacci, Descartes, Fermat, Pascal, Newton, Leibniz, Euler, Gauss, Riemann, Poincaré, Neumann, Turing, and Shannon. For Japanese mathematicians, we think of Takakazu Seki, Teiji Takagi, Kiyoshi Oka, and Yutaka Taniyama. And most recently, there’s Shinichi Mochizuki. All outstandingly talented individuals, and some have strong personalities. Some appear to be loners, similar to the image of a creative genius (such as Kiyoshi Oka). Are these images we have of mathematicians true or false?

The Graduate School of Mathematical Sciences at the University of Tokyo is home to a youthful mathematician who gives the impression that he might be a genius: Professor Yoshikata Kida. After his junior year at Kyoto University, he skipped his senior year to go straight to graduate school. His Doctoral dissertation attracted a great deal of attention and made him a household name in the world of mathematics. After obtaining his Ph.D., he worked at the Max Planck Institute in Germany, Tohoku University, and Kyoto University, before becoming a professor at the University of Tokyo in his thirties. His soft smile is warm and sincere, and he gives no hint of being a genius with an intense personality. What abyss is he looking into?
I call my research topic ergodic group theory.
Professor Kida is researching a topic known as group theory. Amateur mathematicians like us can only comprehend the vague notion that a ‘group’ is an assembly of numbers that possesses several properties (it can perform a single operation, the associative law holds, it has an identity element, and it has an inverse).
“Oh, yes. By definition, ‘group’ is an algebraic concept. However, it also includes a geometric perspective. People often ask me, ‘What is a group used for?’ I tell them by way of example that a group can be thought of as an indicator of the beauty of a figure. Everyone has their own subjective impression of what the word ‘beauty’ means, but if you compare a circle, a triangle, and a quadrilateral, for instance, the circle is the most beautiful, because it has no angles. It’s the concept of a group that allows us to represent this beauty.”
An equilateral triangle can be rotated and superimposed exactly on itself three times. Simply rotate it by 120 degrees each time. A square can be rotated through 90 degrees and superimposed exactly on itself four times. The greater the number of possible superimposition operations, the more beautiful it is. All circles can be superimposed exactly on themselves no matter how many times you rotate them. So that’s why the circle is the most beautiful. The set of such superimposition operations is also a group.
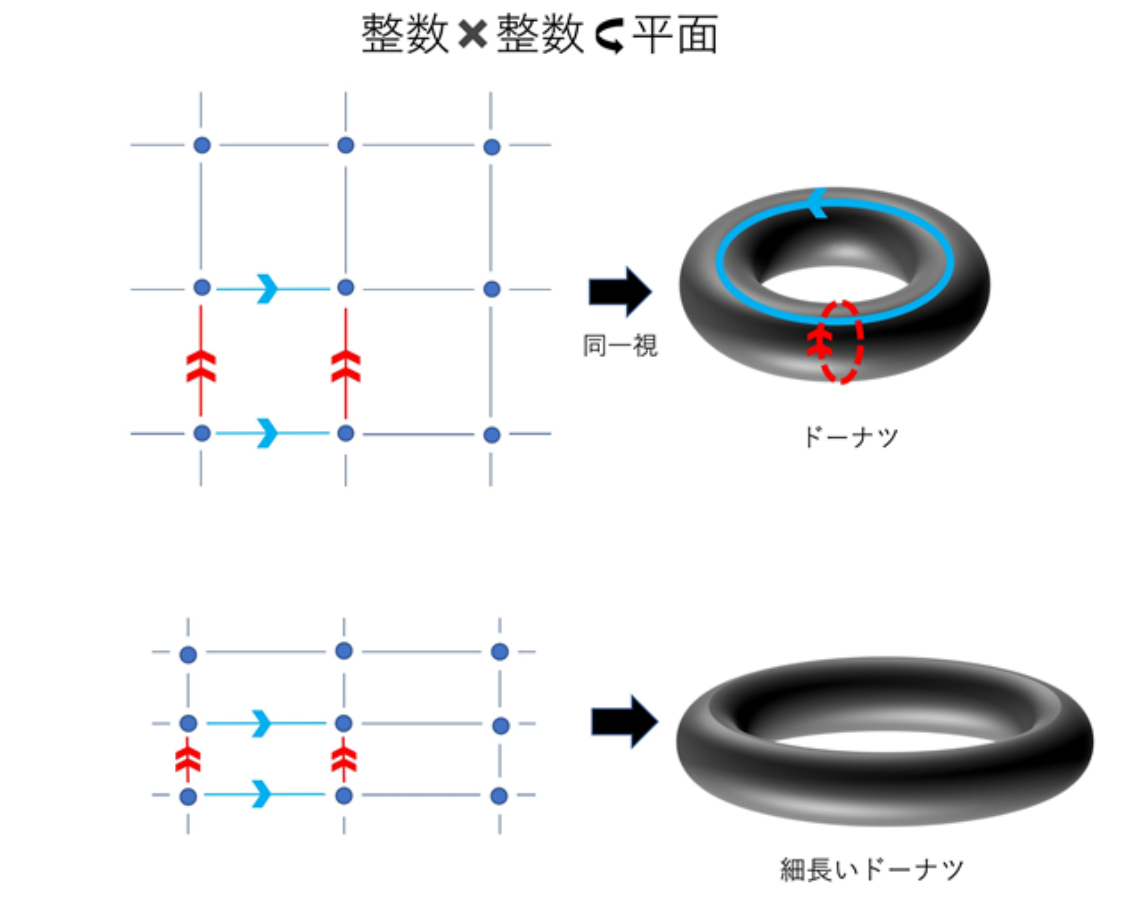
“Many mathematical problems can be formulated in the language of groups. We can better understand the original problem by expressing it in terms of groups. So, groups play a fundamental linguistic role across the whole of mathematics. For example, consider a number of ‘integer points’ on a plane, and think of them as a series of squares. If you move one point in the vertical direction and one point in the horizontal direction, the two are regarded as equivalent. If you continue this process, it will produce the shape of a donut. In this way, the problem of the geometry of a donut can be replaced by ‘how to embed a group in a plane of size integer × integer’.”
In other words, groups can be used as mathematical tools, and may be found in almost any field. So what does Professor Kida’s research topic have to do with these groups?
“My research involves something called discrete groups. In addition to the ‘integer × integer’ problem we were talking about, there are many more sporadic discrete groups. The topic comes up in various areas of mathematics. If two discrete groups can be embedded in a lattice form in a continuous group, we say that they are equivalent. My research involves categorizing discrete groups in this way”.
When I was looking for Professor Kida’s writings on the Web, I found the following statement: “I have decided to call my research topic ‘ergodic group theory.’”
“Oh, yes. I call my research topic ‘ergodic group theory.’ Groups are algebraic according to their original definition, but in the 1990s the mathematician Mikhael Gromov introduced a geometric perspective to group theory and created the field of geometric group theory. My research is in a field which is like a sibling of geometric group theory. In English, it’s called measured group theory, but I thought the translation into Japanese was kind of uncool, so I decided to call it ergodic group theory. We investigate how to understand the world of all discrete groups using ergodic theory, which is a field of mathematics that deals with the action of a group on a space with measure. I study discrete groups using such actions on spaces with measures.”
If you search the Web, you will find many explanations of geometric group theory, measures, ergodic theory, and so on. Interested readers are encouraged to check them out.
After a painfully tough period of research, an idea suddenly emerged.
Mathematics can be divided into two broad types—pure and applied—and Professor Kida focuses on the former type. As the name suggests, it’s a pure field of study, in which theories of mathematics itself are developed. Abstract thinking is deepened through mathematical expressions. Applied mathematics, on the other hand, is a field in which mathematics is used to deal with events in the real world. Starting with the description of natural phenomena using mathematics, its practitioners use mathematics to describe various aspects of society.

For more than 20 years, advanced mathematical techniques have been used in the trading of financial products such as derivatives, and mathematics also holds the key to weather simulations and the recently popular field of data science (often in the form of mathematics plus computational science). From the point of view of the layperson, applied mathematics is easy to conceptualize because it involves concrete events, even if it’s methods can’t be understood. However, pure mathematics appears to be an abstract world, through and through. Do pure mathematicians have an image in their mind before they come up with a mathematical expression?
“I’m not aware that I’m doing anything abstract at the beginning. I start with a concrete image that can be represented graphically, such as embedding integers in a plane, as I mentioned earlier. However, when you write a paper, you start with the bare minimum description necessary to get to the real answer, so that may seem more abstract.”
Professor Kida, who I had thought looked like a genius, suddenly seemed less remote. Let’s ask him a down to earth question. Was he thinking about becoming a mathematician when he was in high school?
“No way! Not at all (laughs). When I was in high school, I liked mathematics and physics, and I loved solving problems. I’d be happy when I could solve a difficult problem, but I didn’t feel like this was what I wanted to pursue in the future. Even after I went to university, I used to just say that I enjoyed it. As a university student, however, I looked at mathematics in a totally different light than I did in high school. I used to enjoy looking at mathematics books in the library and thinking about how many different kinds of mathematics there were. However, that all changed when I became a graduate student.”
As a young graduate student, Kida suddenly found mathematics difficult, because instead of just solving problems and reading books for enjoyment, he now had to do research.
“Until then, all I’d done was solve problems, but now that I was a graduate student, I had to write research papers, so I had to find a topic to explore. In other words, you have to create your own problems. ‘Why don’t you check out these papers?’ my supervisor recommended, but even after reading them, I just couldn’t seem to write my own. It was a real struggle. When I was in the first year of my Master’s program, I still had a lot of spare mental capacity (laughs), but in the second year, I started to feel like I’d hit a wall and couldn’t go any further. I thought that the only way to make progress was through imitation, so I scoured papers that I thought I could imitate and kept thinking, ‘I wonder whether I could tweak this just a little.’ Ultimately, I somehow managed to finish my Master’s thesis and then write my Doctoral thesis. Relieved to have finished writing, I was reading a survey article by Nikolai Ivanov when I had a sudden flash of realization, ‘Aha! It was like a lightning strike!’”
I guess you could call this a revelation. The youthful Kida had a Eureka moment.
“I remember being pretty excited. It may be the only time in my mathematical life that I have ever had an ‘epiphany,’ and it may never happen again. In the end, I spent the first half of my stay at Max Planck whipping the idea into shape. Fortunately, the paper I wrote on the basis of that idea was well-received by prominent mathematicians.”
Pure mathematicians also have connections with the real world.
A thesis written after a flash of inspiration. Was that the time when he wanted to become a mathematician?
“I decided to become a mathematician after completing my Doctorate and spending a year at the Max Planck Institute in Germany. When I’d applied for the position there, I’d thought, ‘If I don’t get in, I’ll find another career path instead of aiming to be a mathematician.’ Next, Tohoku University hired me as an Assistant Professor, and that’s when I became a mathematician.”
Given his résumé, he appears to be a genius, but he had to overcome anguish and pain before becoming a mathematician. So, I guess it was only after he was hired as a researcher that he was ready to be a mathematician.
“I had a difficult time during my Master’s, so I wouldn’t say that I wasn’t frustrated. In fact, I still find mathematics research to be a painful undertaking. My workload as an educator is increasing, and I have a family to take care of. I cook meals at home, among other things (laughs). You need physical strength to concentrate on research. After all, the inspiration came to me in the best of circumstances, when I had the physical strength and time available to handle it.”
Just as it’s difficult for an athlete to keep winning gold medals, it must be tough for a mathematician to keep turning out remarkable results. A pure mathematician who struggles alone to achieve results. It’s only natural that the general public will have an image of the mathematician as a solitary figure. As a pure mathematician, how does Professor Kida feel about the larger number of his colleagues working in applied mathematics?
“I am honestly envious of applied mathematicians who can apply their mathematics to society and make people happy. As a matter of fact, I’m the only Japanese mathematician who specializes in ergodic group theory, as I mentioned earlier (laughs). To put a favorable spin on it, my work is ‘highly original,’ but in a negative sense, I’m ‘working in a very small world.’ Sometimes when I talk about my achievements to people in a similar field, they don’t understand what I’m doing, or appreciate my difficulties. However, I don’t think of myself as being solitary or independent. If I remain fixed in the abstract world of pure mathematics, I sometimes get stuck. At such times, I look for a different topic: for example, I often get hints and motivation from nature to come up with a new topic. In other words, even pure mathematicians have connections to the real world.”
A pure mathematician who is connected to the real world. You can appreciate that there’s a novel just in that narrative.

Acquire diverse mathematical values.
I have to say that it’s fascinating to listen to a pure mathematician, albeit for a short time, who seems to carry the rationality of the world on his shoulders. It’s no wonder that many high school students, examinees, and undergraduate students in the world want to become mathematicians. What is your message to these young people who aspire to be mathematicians?
“Hmmm... if I had to sum it up in one sentence, I would say, ‘Acquire diverse mathematical values.’ Compared with what high school students know about the subject, the world of mathematics is very wide, deep and diverse. That’s why I want you to be exposed to university mathematics and other areas, to learn about different types of mathematics, and to broaden your mathematical values. It will also influence the way you set up your own problems later on. I also want you to talk about mathematics with your friends, because everyone has different values. If you’re a high school student or an examinee, talk about mathematics with your math-loving friends, or with your classmates if you are an undergraduate student of mathematics. Even if you’re discussing a simple mathematical fact that you were familiar with, you’ll find that there are others who think deeply about it.
Diverse mathematical values. ....... Just as philosophers approach the world’s abyss, mathematicians do likewise with their own values. So, what lies ahead?
When you become a mathematician, you will surely be able to witness the future.
※Year of interview:2022
Interview/Text: Osamu Shimizu [ ACADEMIC GROOVE ]
Photography: Junichi Kaizuka

![リガクル[RIGAKU-RU] Exploring Science](/ja/rigakuru/images/top/title_RIGAKURU.png)









