ボードゲームのはなし

伊藤 創祐（生物普遍性研究機構 講師）

寒くなってくるとボードゲームの季節だな，と思う。というのも，ドイツ年間ゲーム大賞をとったボードゲームの日本語版が，冬頃に広く出回るからだ。この大賞をとったボードゲームで遊ぶのが，私にとっての冬の風物詩だ。

大賞をとるようなボードゲームにもさまざまなタイプのものが存在するが，人気になるボードゲームはおよそ次のような性質を持つ。まずダイスの目やカードのシャッフルなどでランダム性が発生する。次にゲーム内のリソースを消費して，このランダム性に対するギャンブルを行う。そして，その下で勝利点を集めて勝利する。よってボードゲームの勝敗は，このギャンブルに対して最適な戦略を取れたかどうかの答え合わせだ。自分が組んだ戦略の良し悪しを感想戦で議論するのは，ボードゲームの醍醐味の一つだろう。

さてボードゲームでのランダム性は，ダイスの目やカードのシャッフルなどの物理的な過程に起因する。物理的な過程でランダム性が起きる以上，ランダム性の下で適切な戦略を取って「勝利点」を集める「ボードゲーム」は物理学の対象になりうる。ただしこの「ボードゲーム」における「勝利点」とは，熱機関における仕事であったり，正確な情報通信における伝送レートであったり，細胞の進化における適応度であったりする。適切な設定のもとで，これらの勝利点をいかに集めるか，最適な戦略をとったときに勝利点の期待値はどれだけか，ということを数式を使って考えると研究になる。

そもそも歴史的にもランダム性が関わる学問とギャンブルは相性がいい。たとえば，確率論はそもそもブレーズ・パスカル（Blaise Pascal）とピエール・ド・フェルマー（Pierre de Fermat）らによるギャンブルの話題から始まったという。 現在でもギャンブルと結びつけて現代的な確率論を構築するゲーム論的確率論も存在する。また情報理論はクロード・エルウッド・シャノン（Claude Elwood Shannon）による通信の数学的理論として出発したが，その後ジョン・ラリー・ ケリー・ジュニア（John Larry Kelly, Jr）によってギャンブルでの儲けの期待値の限界という観点から再定式化された。

ここからは個人的な研究の話である。このケリーの情報理論は一般的な枠組みのため，物理的な実在に対するギャンブルにも適用可能である。そこで分子の運動のランダム性に対して，仕事を取り出すことを勝利点とするギャンブルとして，マクスウェルのデーモン^注1 という熱力学の話を捉えることができる。

ある種のフェアなギャンブルで1/2の確率でサイコロの偶奇を当てることで かけた額の2倍の勝利点を手に入れることができるように，マクスウェルの デーモンの話においては1/2の確率で粒子の左右の位置を当てることで，粒 子がいる領域の体積を仕切りを動かして2倍にでき，kBTln2の仕事を取り出すことができる（Tは箱に接触した熱浴の温度，kBはボルツマン定数）。ここでln2という量は、1/2の確率の状態を事前に知っている時の情報に対応する。

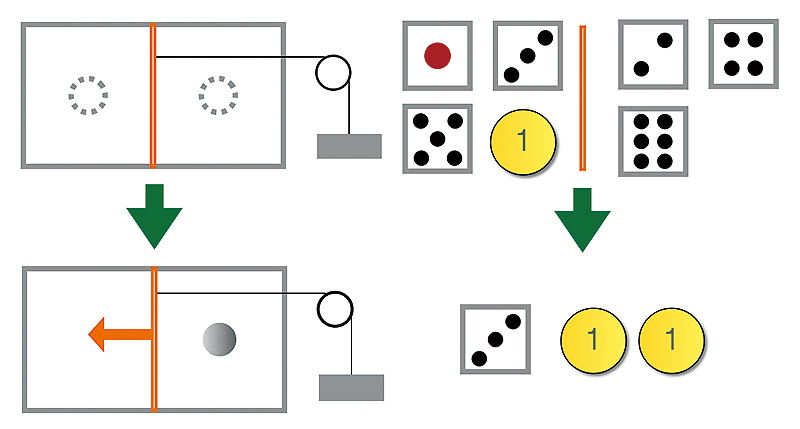
学生の頃マクスウェルのデーモンの研究をしていてこの考え方に到達し，それから数年後に様々な知見を合わせて，とある論文の中で情報の流れを含んだ熱力学第二法則の一般化とケリーの情報理論との関係を述べるに至った [S. Ito, Sci. Rep. 6, 36831 (2016).]。ボードゲームで培ってきたものの見方が，研究にまで影響を及ぼしたという一例である。

2021年現在，対面で集まって何かをすることがしにくい社会的状況である。しかしながらボードゲームにはさまざまな オンラインツールが存在するので，それを使ってオンライン飲み会ならぬオンラインボードゲーム会をするのは一興である。ボードゲームならば全員が能動的に参加するので，やってみるとオンライン飲み会よりも盛り上がったりする。親交を深めづらいこのご時世，オンラインボードゲーム会と洒落込んで交流を深めてみるのはいかがだろうか。